Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 4.4 - Ex. 26
Uma pedra é lançada por uma catapulta no instante , com uma velocidade inicial de módulo e ângulo acima da horizontal. Quais são os módulos das componentes (a) horizontal e (b) vertical do deslocamento da pedra em relação à catapulta em ? Repita os cálculos para as componentes (c) horizontal e (d) vertical em s e para as componentes (e) horizontal e (f) vertical em .
Passo 1
Então galera, a pedra ao ser lançada irá descrever um lançamento obliquo, e por conta disso esse movimento pode ser dividido em movimento uniforme em relação ao eixo e movimento uniformemente variado em relação ao eixo .
O deslocamento em um movimento uniforme pode ser obtido através da relação:
E essa será a componente do deslocamento na horizontal.
No movimento uniformemente variado, por sua vez, o deslocamento pode ser obtido através da fórmula:
E assim, vamos escrever a componente do deslocamento na vertical.
Beleza pessoal, agora precisamos definir a velocidade incial da pedra em relação aos dois eixos para usarmos nessas fórmulas. Para isso faremos a decomposição do vetor velocidade inicial:
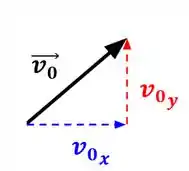
Como o enunciado nos informa o ângulo de lançamento é em relação a horizontal, obtemos que:
Passo 2
Agora basta substituirmos os valores de velocidade encontrados anteriormente e os valores de tempo indicados em cada item.
Sabemos que o ângulo de lançamento é de em relação a horizontal, o tempo é e a velocidade inicial , substituindo nas equações teremos que:
m
Passo 3
Item (c) e (d)
Agora nós repetimos o processo utilizando as mesmas equações, mas dessa vez para :
Passo 4
Item(e) e (f)
Nesses dois últimos itens tem uma pegadinha. A questão é que a pedra chega ao solo antes dos . Por isso é sempre importante calcularmos o momento em que ocorre a queda pra gente não errar bobeira.
Vamos primeiro descobrir em que instante a pedra chega ao solo. Para isso vamos isolar o tempo na equação da componente:
Logo, como a pedra chegou ao chão, consideramos que sua posição é , com isso obtemos que:
Podemos cortar um de cada lado, ficando com:
Substituindo agora os valores conhecidos, ficamos com:
Agora bora calcular a componente horizontal da posição quando a pedra chega ao solo ():