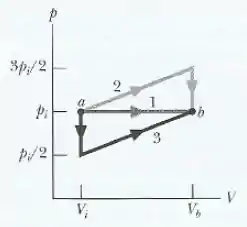
Uma amostra de gás sofre uma transição de um estado inicial a para um estado final b por três diferentes trajetórias (processos), como mostra o diagrama p - V da figura, onde V b = 5,00 V i . A energia transferida para o gás como calor no processo 1 é 10 p i V i . Em termos de p i V i , qual é (a) a energia transferida para o gás como calor no processo 2 e (b) a variação da energia interna do gás no processo 3 ?

(a) Q 2 = 11 p i V i (b) Δ U 3 = 6 p i V i

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 18.Problemas Adicionais - Ex. 81

Uma amostra de gás sofre uma transição de um estado inicial para um estado final por três diferentes trajetórias (processos), como mostra o diagrama da figura, onde . A energia transferida para o gás como calor no processo é . Em termos de , qual é (a) a energia transferida para o gás como calor no processo e (b) a variação da energia interna do gás no processo ?

Passo 1

Nós temos 3 processos distintos entre si mas que têm os mesmos estados inicial e final. Como a variação de energia interna não depende do caminho para processos reversíveis então vamos ter que

E é a partir daqui que vamos resolver esse problema, beleza?

Passo 2

Escrevendo a primeira lei da termodinâmica para os processos 1 e 2

A letra (a) pede o calor da etapa 2, logo

O enunciado já nos disse que , então nos falta e .

Passo 3

Para calcular e , podemos calcular a área abaixo de cada uma dessas curvas no diagrama !

O processo é isobárico, logo a área abaixo da sua curva é um retângulo, assim

Já o processo 2 tem como área um trapézio de base menor e base maior e altura , assim

Agora podemos calcular o calor do processo 2

Passo 4

A variação de energia do processo 3 é igual à variação de energia interna do processo 1

Como já temos todas as informações do processo 1

Resposta

(a)

(b)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O diagrama p - V da figura mostra duas trajetórias ao longo das quais uma amostra de gás pode passar do estado a para o estado b , no qual V b = 3,0V 1 . A trajetória 1 requer que uma energia igual a

Em um motor de motocicleta, um pistão é empurrado para baixo, na direção do virabrequim, quando o combustível que está no cilindro entra em ignição, e a mistura de gases da combustão se expande adiaba

Um sistema termodinâmico vai do estado a até o estado c mostrado na Figura 19.29 pelo caminho a b c , o trabalho W realizado pelo sistema é igual a 450J . pelo caminho a d c , W é igual a 120J . As en

Três mols de um gas ideal passam pelo ciclo a b c mostrado na Figura 19.31. O C P desse gás é 29,1J / m o l ⋅ K . O processo a c ocorre sob pressão constante, o processo b a a volume constante e o pro

Quando um sistema vai do estado a até o estado b (Figura 19.28) pelo caminho a c b , um calor igual a 90,0J flui para o interior do sistema, e um trabalho de 60,0J é realizado pelo sistema. a) Qual é