Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 19.Problemas - Ex. 48
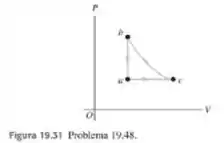
Três mols de um gas ideal passam pelo ciclo mostrado na Figura 19.31. O desse gás é . O processo ocorre sob pressão constante, o processo a volume constante e o processo é adiabático. As temperaturas do gás nos estados e são , e . Calcule o trabalho total do ciclo.
Passo 1
O trabalho total vai ser a soma do trabalho de cada processo, como no processo o volume não varia, o trabalho dele vai ser zero:
Ficamos então com:
Passo 2
Vamos calcular primeiro , que é o processo adiabático, e por isso:
Então a primeira lei da termodinâmica para esse processo, fica:
A variação da energia interna pode ser calculada por:
Como temos , vamos usar a relação:
Para substituirmos :
Substituindo os valores:
E o trabalho desse processo fica:
Passo 3
Para o outro processo, como a pressão é constante, podemos usar a relação:
Mas como não temos o valor da variação de volume, vamos usar a equação de um gás ideal:
E igualar com o trabalho:
Porque temos as temperaturas.
Substituindo os valores:
Passo 4
Agora podemos somar tudo para conseguir o trabalho total: