Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 15.1 - Ex. 18
Em um ancoradouro, as marés fazem com que a superfície do oceano suba e desça uma distância (do nível mais alto ao nível mais baixo) em um movimento harmônico simples com um período de . Quanto tempo é necessário para que a água desça uma distância de a partir do nível mais alto?
Passo 1
Estamos pensando nas marés como se fossem um movimento harmônico simples da superfície do oceano. Vamos ver o que a questão deu de informação.
Se é a distância do nível mais alto ao nível mais baixo, a gente sabe que ele é o dobro da amplitude. Ou seja:
Se isso te confundir, lembre sempre de um pêndulo:
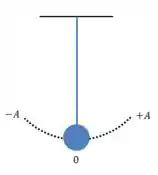
A amplitude é sempre metade do caminho total percorrido pelo objeto executando o movimento harmônico simples. Beleza? Vamos em frente.
Passo 2
Agora vamos usar o período de pra encontrar a frequência angular, e assim completar a função da posição.
Precisamos passar esse valor pra segundos:
E agora:
Passo 3
Continuando a completar a função:
Como a questão quer a resposta “a partir do ponto mais alto”, a constante de fase é .
Por quê? Se é “a partir do ponto mais alto”, então quando , tem que ser o ponto mais alto, ou seja:
E isso só acontece se .
Agora sim chegamos na função completa:
Passo 4
E o problema é só achar de forma que:
Qual ângulo tem cosseno igual a ? Têm vários, mas o menor é o , como queremos o menor tempo necessário, vamos pegar esse ângulo.
Resolvido!
Resposta
São necessários aproximadamente .