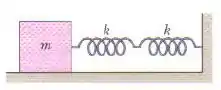
Na figura, duas molas são ligadas entre si e a um bloco de massa que oscila em um piso sem atrito. As duas molas possuem uma constante elástica . Qual é a frequência das oscilações?

Agora vamos imaginar que o bloco ande um pouco pra esquerda, a força que puxa o bloco pra direita é a mesma nas duas molas, certo?

Então pela lei de Hooke a gente pode afirmar que:

O que não quer dizer que as deformações e são iguais, ok? Só que esses produtos aí são iguais.

E quando juntamos com a equação ali de cima, chegamos na seguinte igualdade final:

Nosso objetivo é achar em termos de e . Se mexermos um pouco nos dois primeiros termos da igualdade, vamos achar o seguinte:

E agora pegando os dois últimos termos:

Substituindo:

Agora cortando :

Beleza, achamos a fórmula que queríamos.

Agora podemos substituir os valores. As duas molas tem constantes elásticas :

E como a massa é , podemos achar a frequência angular:

E a frequência de oscilação é:

Pronto!