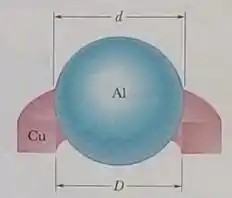
Um anel de cobre de a tem diametro interno . Uma esfera de aluminio a tem um diametro . A esfera é colocada acima do anel até que os dois atinjam o equilíbrio térmico, sem perda de calor para o ambiente. A esfera se ajusta exatamente ao anel na temperatura de equilíbrio. Qual é a massa da esfera?

Fala galerinha do RespondeAí, tudo jóia?

Saca só, nesse exercício aqui o enunciado nos diz que um anel de cobre de a tem diâmetro interno , ele continua dizendo que uma esfera de alumínio a tem um diâmetro . E sabendo que a esfera é colocada acima do anel até que os dois atinjam o equilíbrio térmico, de modo que a esfera se ajusta exatamente ao anel, sem perda de calor para o ambiente, o enunciado nos pergunta qual é a massa da esfera!

Uma malandragem pra gente começar o problema, é que a variação de temperatura em Celsius é igual à variação em Kelvin, logo, não precisaremos nos preocupar com isso nesse problema, pois as fórmulas que vamos usar só precisam da variação da temperatura, ok?

Lembra como varia o tamanho de um material em função do seu coeficiente linear de dilatação térmica Varia assim:

Sendo o seu comprimento inicial e a variação de temperatura envolvida.

Substituindo o diâmetro do anel nessa relação, a gente obtém essa equação aqui:

Para a esfera, temos:

Como, ao final, o anel e a esfera se ajustam, o tamanho final do diâmetro dele é igual:

E, então, podemos igualar as duas equações dos diâmetros finais:

Vamos arrumar um pouquinho, nosso intuito é isolar o :

Vamos jogar tudo que tem para um lado e o resto para o outro:

Colocando em evidência:

Com isso:

Vamos passar os diâmetros para metros ok? É só multiplicar o valor original por . Além disso, vamos pegar os valores dos coeficientes de dilatação na tabela 18-2 do livro.

Substituindo aí os dados do enunciado, vem:

Fazendo essa conta monstro: