Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 15.1 - Ex. 91

Um apito com frequência de 500 Hz se move em um círculo de raio de 1,00 m a 3,00 rev / s. Quais são as frequências máxima e mínima ouvidas por um ouvinte estacionário no plano do círculo e a 5,00 m de distância do centro?

Passo 1

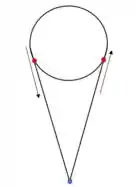
As frequências máxima e mínima estão representadas na imagem abaixo, os pontos vermelhos são as posições do apito para os dois casos, e as setas representam o vetor velocidade do apito naquele instante, quando ele aponta para o ponto azul que é a posição do ouvinte, a frequência da onda é máxima e quando a seta está oposta ao ponto azul, ela é mínima:

Passo 2

Dessa forma, podemos usar a equação do efeito Doppler para determinarmos a frequência da onda ouvida pelo ouvinte (receptor):

f m á x = v ± u r v ± u e f e

Como o receptor está parado u r = 0 , e no caso da frequência máxima, o apito está se aproximando do receptor, então o sinal é negativo no denominador, ficamos com:

f m á x = v v - u e f e = 1 1 - u e v f e

Podemos escrever u e = r ω , por causa do movimento circular do apito

f m á x = 1 1 - r ω v f e

Substituindo os valores numéricos para cada grandeza:

f m á x = 1 1 - 3.00 r e v / s × 2 π r a d r e v 343 m / s 500 H z

f m á x = 529   H z

Passo 3

Para a frequência mínima, a equação ficará:

f m i n = v v + u e f e = 1 1 + u e v f e

f m i n = 1 1 + 3.00 r e v / s × 2 π r a d r e v 343 m / s 500 H z

f m i n = 474   H z

Resposta

f m á x = 529   H z

f m i n = 474   H z

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um trompetista em um vagão de trem em movimento se aproxima de um segundo trompetista ao lado dos trilhos enquanto ambos tocam uma nota de 440 H z . As ondas sonoras ouvidas por um observador estacion
Uma fonte sonora se move ao longo de um eixo x , entre os detectores A e B . O comprimento de onda do som detectado por A é 0,5 do comprimento do som detectado por B . Qual é a razão v F / v entre a v
Um carro de polícia persegue um Porche 911 por excesso de velocidade. Suponha que a velocidade máxima do Porche é 80 m / s e a do carro de polícia é 54 m / s . No instante em que os dois carros atinge
Uma fonte pontual que está parada em um eixo x emite uma onda sonora senoidal com uma frequência de 686 H z e uma velocidade de 343 m / s . A onda se propaga radialmente, fazendo as moléculas de ar os
Um submarino francês e um submarino norte-americano se movem um em direção ao outro durante manobras em águas paradas do Atlântico Norte. O submarino francês se move com uma velocidade v F = 50 k m /