Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 49
APLICAÇÃO EM ENGENHARIA. Um carro de tração traseira suporta por cento de seu peso sobre suas duas rodas de tração e tem um coeficiente de atrito estático de com uma estrada reta horizontal, (a) Encontre a aceleração máxima do veículo. (b) Qual é o menor tempo que este carro leva para atingir uma rapidez de ? (Considere um motor capaz de suprir potência sem limites.)
Passo 1
A força de atrito que a estrada exerce sobre os pneus proporciona força líquida que acelera o carro. A representação esquemática das forças está abaixo. Podemos usar a segunda lei de Newton para determinar a aceleração do carro e a equação horária da velocidade para calcular quanto tempo demora para chegar a .
Passo 2
Item (a)
Como 40% do peso do carro está em suas duas rodas motrizes e a força de atrito age apenas nestas rodas, o diagrama de corpo livre abaixo mostra apenas as forças que atuam nas rodas motrizes.
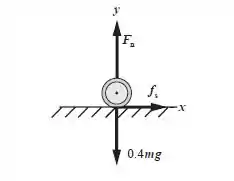
De acordo com a 2° Lei de Newton no eixo x:
E a 2° Lei de Newton em y, como a soma das forças em y é igual a zero, pois o carro não sobe nem desce na pista no eixo y, então:
Como temos:
Substituindo por valores numéricos:
Passo 3
Item (b)
Usando a equação horária da velocidade:
Consideraremos a velocidade inicial e , então:
Substituindo pelos valores que temos: