Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 26
APLICAÇÃO EM ENGENHARIA. Para determinar o arraste aerodinâmico sobre um carro, engenheiros automotivos usam frequentemente o método "do ponto morto". O carro é colocado a percorrer uma estrada longa e rela, a uma rapidez conveniente (tipicamente ) e, mantido em ponto morto, acaba por parar. O tempo que o carro leva para que a rapidez decresça de intervalos sucessivos de é medido e usado para calcular a força resultante que o freia. (a) Um dia, um grupo constataram que um Toyota Tercel com de massa levou para reduzir de para . Estime a força resultante média que freou este carro, nesta faixa de valores de rapidez. (b) Se é sabido que o coeficiente de atrito de rolamento para este carro vale , qual é a força de atrito de rolamento que atua para freá-lo? Supondo que as únicas duas forças que atuam sobre o carro são o atrito de rolamento e o arraste aerodinâmico, qual é a força média de arraste aerodinâmico atuando sobre o carro? (c) A força de arraste tem a forma . onde é a área de seçào reta que o carro expõe ao ar, é a rapidez do carro, é a massa específica do ar e é uma constante adimensional da ordem de grandeza de 1. Se a área de seção reta do carro é , determine C a partir dos dados fornecidos. (A massa especifica do ar é use para a rapidez do carro. neste cálculo.)
Passo 1
As forças que atuam no Tercel à medida que diminui de para são uma força de atrito exercida pela estrada, que chamaremos de força de rolamento, uma força de arrasto exercida pelo ar, a força normal exercida pela estrada e a força gravitacional exercido pela Terra. O carro está se movendo na direção x positiva. Podemos usar a Segunda lei de Newton para calcular a força média a partir da taxa em que o a velocidade do carro diminui, isto é, a aceleração. A força de arrasto pode ser inferida a partir da força rolamento e do coeficiente de arrasto da equação que define a força de arrasto. Olhe a figura abaixo para ver o esquema das forças que atuam no carro:
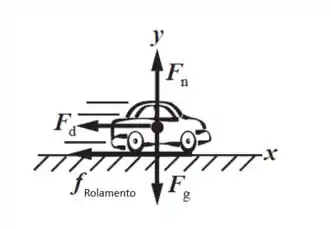
Passo 2
Item (a)
Como o carro não vai para cima nem para baixo, apenas para frente, então o somatório das forças em y é igual a zero. Portanto, só nos interessa as forças em x:
Porém, podemos calcular a força média através da fórmula:
Em que é a massa do carro, é a variação de velocidade e é a variação de tempo. Então, através dos valores dados pelo enunciado:
Passo 3
Item (b)
A força de atrito de rolamento é a produto do coeficiente de atrito de rolamento e a força normal:
Substituindo os valores numéricos que já temos:
Assumindo que as duas forças que estão reagindo no carro com o sentido oposto ao movimento do carro são a força de rolamento e a de arrasto:
Sendo a força de arrasto, substituindo os valores que já temos para e :
Passo 4
Item (c)
Usando a definição de força de arrasto dada no enunciado e o valor calculado no item b, temos: