Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 36
Uma caixa pesando 600 N é empurrada sobre um piso horizontal, com velocidade constante, por uma força horizontal de 250 N paralela ao piso. Qual é o coeficiente de atrito cinético entre a caixa e o piso?
Passo 1
Olá, querido! Temos uma caixa com velocidade constante, ou seja, não há aceleração na direção do movimento .
E ela é puxada por um lado por uma força constante . Só que o enunciado diz que há atrito cinético. Ele vai se opor ao movimento, então temos uma força de atrito que vai apontar para o sentido inverso de . Um esquema dessa situação é:
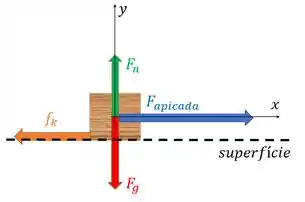
Temos força peso e temos força normal por causa do contato entre bloco e superfície.
A caixa já está deslizando, então o tipo de atrito em questão é o atrito cinético. E a pergunta que ele nos faz é: quanto vale o coeficiente de atrito cinético ?
Vamos descobrir!
Passo 2
A gente precisa relacionar as forças atuando nessa caixa para achar . Aplicando a segunda lei de Newton para a direção vertical vamos ter
Só que a caixa não sobe nem desce, então .
O somatório de forças na vertical é porque está no sentido negativo de , assim substituindo isso na lei:
Passo 3
Agora para a direção :
Mas lembra de algo bem importante: por a velocidade do bloco ser constante, aceleração dele é nula . Substituindo isso:
Falta montar o somatório de forças em . Vai ser:
A força tem sinal de menos porque aponta para a parte negativa de e é positiva porque aponta para parte positiva de . Substituindo na segunda lei:
Passo 4
Só que o atrito é cinético, e ele tem essa fórmulinha:
Vimos que :
E lembrando que :
Isolando o (quem a gente quer)
Agora a gente substitui os valores: