Você e seu melhor amigo fazem uma aposta. Você alega poder colocar uma caixa de 2,0 kg encostada a um dos lados de um carrinho, como na figura abaixo, sem que a caixa caia no chão, mesmo você garantindo que não fará uso de ganchos, cordas, prendedores, ímãs, cola ou qualquer outro tipo de adesivo. Quando seu amigo aceita a aposta, você começa a empurrar o carrinho no sentido mostrado na figura. O coeficiente de atrito estático entre a caixa e o carrinho é 0,60. (a) Encontre a menor aceleração com a qual você vencerá a aposta. (b) Qual é a magnitude da força de atrito, neste caso? (c) Encontre a força de atrito sobre a caixa se a aceleração é duas vezes a mínima necessária para que a caixa não caia. (d) Mostre que, para uma caixa de qualquer massa, a caixa não cairá se a magnitude da aceleração para a frente for , onde é o coeficiente de atrito estático.

Passo 1
Letra (a)
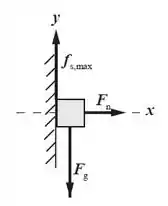
O que deve acontecer é que a aceleração deve ser grande o suficiente para que a força de atrito consiga ser igual ao peso da caixa. Só que quando a aceleração é a mínima possível, a força de atrito estático é a máxima. Pensando nisso, vamo usar a segunda lei de Newton para a caixa em x e em y. Começando com y:
Só que a força de atrito é máxima, lembra? Então . Joga isso na equação:
Passo 2
Agora em x:
Agora junta (2) com (3):
Corta o m e isola o :
Agora joga os valores:
Passo 3
Letra (b)
Olha a equação (1) lá em cima.
Passo 4
Letra (c)
Pensa só: se a aceleração aumantar mais do que o mínimo, o que acontece? A caixa vai cair? Não, porque a aceleração é maior do que o mínimo necessário para não cair. Vai subir? Claro que não kkk, isso aconteceria se a força de atrito ultrapassasse o valor do peso da caixa. A única alternativa que resta é a força de atrito continuar igual ao peso da caixa:
Passo 5
Letra (d)
A gente mostrou na letra (a) que a menor aceleração que impede o bloco de cair é e esse valor não depende da massa. Então se a aceleração for ainda maior que esse valor, o bloco continua não caindo, qualquer que seja essa massa.
Resposta
Letra (a):
Letra (b):
Letra (c):
Letra (d): A aceleração é maior do que a mínima necessária.