Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 17.Exercícios e Problemas - Ex. 1

Considere duas cascas esféricas condutoras concêntricas, de raios R 1 e R 2 > R 1 .

a) Calcule os coeficientes de potencial P 11 , P 22 , P 12 e P 21 e verifique que P 12 = P 21 .

b) Mostre que C - 1 = P 11 + P 22 - 2 P 12 , onde C é a capacitância do par de esferas.

Passo 1

Para achar os coeficientes de potencial, escrevemos a relação

φ 1 = P 11 Q 1 + P 12 Q 2 φ 2 = P 21 Q 1 + P 22 Q 2

Nosso trabalho agora é escrever os potenciais φ 1 e φ 2 em cada condutor!

Vamos considerar o sistema com as duas cascas esféricas:

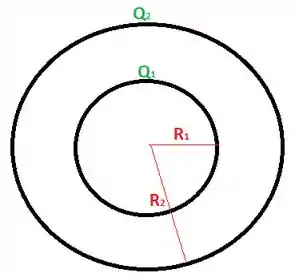
A seguir escrevo a expressão para o campo elétrico em função da distância r ao centro das esferas:

E → r = 0 → ,         r < R 1 1 4 π ϵ 0 Q 1 r 2 r ^ ,               R 1 < r < R 2 1 4 π ϵ 0   Q 1 + Q 2 r 2 r ^ ,             r > R 2

Observe que o campo é nulo para r < R 1 . Esses campos podem ser derivados usando a lei de Gauss e isso já foi feito no capítulo 15 deste livro e nos resumos de RespondeAí! Vamos procurar agora o potencial elétrico φ em função de r considerando que ele é nulo no infinito:

φ r = - ∫ ∞ r E → r ⋅ d r →

Para r > R 2 :

φ r = - ∫ ∞ r 1 4 π ϵ 0   Q 1 + Q 2 r 2   d r = 1 4 π ϵ 0   Q 1 + Q 2 r

Exatamente em r = R 2 nós encontramos:

φ R 2 = φ 2 = 1 4 π ϵ 0   Q 1 + Q 2 R 2

Isso nos leva a

P 21 = 1 4 π ϵ 0 R 2             e           P 22 = 1 4 π ϵ 0 R 2

Passo 2

Agora olhamos para a região entre as cascas esféricas:

φ r = - ∫ ∞ r E → r ⋅ d r → = φ R 2 - ∫ R 2 r E → r ⋅ d r →

Logo,

φ r = 1 4 π ϵ 0   Q 1 + Q 2 R 2 - ∫ R 2 r 1 4 π ϵ 0   Q 1 r 2   d r = 1 4 π ϵ 0   Q 1 + Q 2 R 2 + 1 4 π ϵ 0   Q 1 r - 1 4 π ϵ 0   Q 1 R 2

Note que na integral consideramos o campo da região entre as esferas. Desta forma, para R 1 < r < R 2 :

φ r = 1 4 π ϵ 0 Q 2 R 2 + Q 1 r

Tomando o potencial em r = R 1 :

φ R 1 = φ 1 = 1 4 π ϵ 0 Q 1 R 1 + 1 4 π ϵ 0 Q 2 R 2

Daí, tiramos

P 11 = 1 4 π ϵ 0 R 1           e       ��   P 12 = 1 4 π ϵ 0 R 2

Passo 3

No item (b) queremos mostrar que

C - 1 = P 11 + P 22 - 2 P 12

A capacitância do sistema é dada por

C = 4 π ϵ 0 1 1 R 1 - 1 R 2

Logo,

C - 1 = 1 4 π ϵ 0 1 R 1 - 1 R 2

Por outro lado,

P 11 + P 22 - 2 P 12 = 1 4 π ϵ 0 R 1 - 1 4 π ϵ 0 R 2 - 2 ⋅ 1 4 π ϵ 0 R 2

Portanto,

P 11 + P 22 - 2 P 12 = 1 4 π ϵ 0 R 1 + 1 4 π ϵ 0 R 2 = 1 4 π ϵ 0 1 R 1 - 1 R 2

Com isso, chegamos em

C - 1 = P 11 + P 22 - 2 P 12

Resposta

P 21 = 1 4 π ϵ 0 R 2             e           P 22 = 1 4 π ϵ 0 R 2

P 11 = 1 4 π ϵ 0 R 1           e           P 12 = 1 4 π ϵ 0 R 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Qual é a capacitância de uma gota formada pela fusão de duas gotas esféricas de mercúrio com 2,00 mm de raio?
As placas de um capacitor esférico têm 38,0m m e 40,0m m de raio. (a) Calcule a capacitância. (b) Qual é a área das placas de um capacitor de placas paralelas com a mesma capacitância e a mesma distân
Um capacitor de placas paralelas, cujas placas têm uma área de 8,50c m 2 e estão separadas por uma distância de 3,00 mm, é carregado por uma bateria de 6,00 V. A bateria é desligada e a distância entr
Na experiência de Millikan, uma gota de óleo microscópica, de 2 μ m de raio, é introduzida entre placas de um capacitor plano, cujo espaçamento é de 5c m . A densidade do óleo é de 0,78g/ c m 3 . Com
Dois capacitores, de capacitâncias C e 2 C , estão carregados com a mesma carga Q e inicialmente isolados um do outro. Se as placas negativas de ambos forem ligadas à terra e as positivas ligadas uma