Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 29.1 - Ex. 55

APUCACAO EM ENGENHARIA Ocircuito mostrado na Figura 29-37 e um filtro de corte.(Considere que a saida esteja conectada a uma carga que conduz uma corrente insignificante.)(a)Mostre que o filtro de corte rejeita sinais em uma banda de frequencias centrada ω = 1 / L C b)Como a largura da banda de frequencia rejeitada depende da resistencia R?

Passo 1

Oi oi gente, como vocês estão?

Vamos fazer uma questão passo a passo?

Vamos! Vem comigo.

O diagrama fasorial para o filtro de armadilha é mostrado abaixo. V → a p p  e  V → L + V → c são os fasores de V i n e V o u t , respectivamente. A projeção de   V → app no eixo horizontal é V a p p   = V i n , e a projeção de V → L + V → c no eixo horizontal é V L + V C = V o u t .

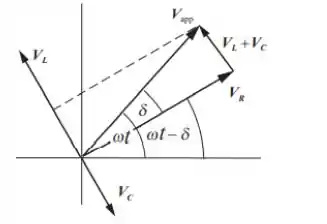
Passo 2

Letra a:

Expresse V a p p :

V app  = V app pico  c o s ⁡ ω t   o n d e   V app.pico  = V pico  = I pico  Z   e   Z 2 = R 2 + X L - X c 2             ( 1 )

V o u t   é dado por:

V out  = V out pico  c o s ⁡ ( ω t - δ )   o n d e   V out, pico = I pico Z trap    e   Z trap  = X L - X C

Resolvendo a equação (1) para Z, temos:

Z = R 2 + X L - X C 2 (2)

Como V out  = V L + V C :

V out  = V out, pico  c o s ⁡ ( ω t - δ ) = I pico Z trap  c o s ⁡ ( ω t - δ ) = V pico Z Z trap  c o s ⁡ ( ω t - δ )

Usando a equação (2) para substituir Z, temos:

V out  = V pico  R 2 + Z trap  2 Z trap  c o s ⁡ ( ω t - δ ) Z trap  = X L - X C = 0

Substituindo X L e X C , temos:

ω L - 1 ω C = 0 ⇒ ω = 1 L C

Passo 3

Letra b:

Seja a largura de banda Δ ω :

Δ ω = ω - ω t a p                       ( 1 )

Seja a largura de banda da frequência definida pela frequência na qual | Z t r a p | = R . Então:

ω L - 1 ω C = R ⇒ ω 2 L C - 1 = ω R C

Porque ω t r a p = 1 L C :

ω ω trap  2 - 1 = ω R C

Para ω ≈ ω t r a p :

ω 2 - ω t r a p 2 ω t r a p ≈ ω t r a p R C

Resolva para ω 2 - ω t r a p 2 :

ω 2 - ω t r a p 2 = ω - ω t a p ω + ω t a p

Como ω ≪ ω t r a p ,   ω + ω t r a p ≈ 2 ω t r a p : :

ω 2 - ω t a p 2 ≈ 2 ω t a p ω - ω t r a p

Substitua na equação (3) para obter:

Δ ω = ω - ω t r a p = R C ω t r a p 2 2 = R 2 L

Resposta

  1. ω L - 1 ω C = 0 ⇒ ω = 1 L C
  2. Δ ω = ω - ω t r a p = R C ω t r a p 2 2 = R 2 L
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

26 - Os componentes de R L C em série possuem os seguintes valores: L = 20,0m H , C = 140n F e R = 350 Ω . O gerador possui tensão eficaz de 120 V e frequência de 1,25k H z . Determine (a) Potência fo
29 - Um circuito RLC em série com L = 0,120 H , R = 240 Ω e C = 7,30μ F conduz uma corrente eficaz de 0,450A A uma frequência de 400H z . Calcule o ângulo de fase e o fator de potência do circuito.Qua
74 - (a) Para qual frequência angular a amplitude da voltagem através do resistor atinge seu valor máximo em um circuito R-L-C em série?
74 - (b) Para qual frequência angular a amplitude da voltagem através do indutor atinge seu valor máximo em um circuito R-L-C em série?
74 - (c) Para qual frequência angular a amplitude da voltagem através do capacitor atinge seu valor máximo em um circuito R-L-C em série?