Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 3.3 - Ex. 19
Mark McGwire bate uma bola de beisebol de forma que ela abandona o bastão com velocidade de formando um ângulo de acima da horizontal. Despreze a resistência do ar. a) Ache os dois instantes para os quais a altura da bola está a acima do nível inicial. b) Calcule o componente vertical e o componente horizontal da velocidade da bola em cada um dos dois tempos calculados no item (a). c) Determine o módulo, a direção e o sentido da velocidade da bola quando ela retorna ao nível inicial.
Passo 1
E aí, galerinha!
Nesse problema temos um batedor de baseball que rebate uma bola com velocidade inicial de a um ângulo de com a horizontal.
A partir daí temos que achar os dois instantes para os quais a altura da bola está a acima do nível inicial, calcular o componente vertical e o componente horizontal da velocidade da bola em cada um dos dois tempos calculados no item (a), determinar o módulo, a direção e o sentido da velocidade da bola quando ela retorna ao nível inicial.
Muita coisa, não é?
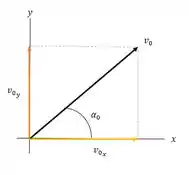
Primeiro, vamos encontrar os componentes e da velocidade inicial.
Vamos adotar as coordenadas onde a direção é para cima, a direção está à direita e a origem está no ponto em que deixa o taco.
Temos que:
Veja só!
Passo 2
Então, temos que:
Bora lá!
Passo 3
Utilizando a componente na vertical, :
Temos que: e queremos saber o tempo, , então vamos utilizar a equação:
Aplicando Bhaskara, temos que:
Sendo:
Portanto,
A bola está a uma altura de 10,0 acima do ponto em que deixou o bastão quando: .
No tempo mais cedo a bola passa por uma altura de 10,0m à medida que sobe e, mais tarde , passa por 10,0m em seu caminho.
Tranquilo até aqui?
Passo 4
Sabemos que , e o tempo todo, que .
Vamos calcular a velocidade para os dois tempos, e que encontramos no item (a), utilizando a equação:
Para :
é positivo, o que significa que a bola está viajando para cima neste momento do caminho.
Para
é negativo, o que significa que a bola está viajando para baixo neste momento do caminho.
Bacana, não é?
Passo 5
Sabemos que .
Vamos resolver para :
Temos que:
Como não precisamos do tempo, vamos utilizar a equação de Torricelli:
Show?
Passo 6
Agora, podemos calcular o modulo e a direção da velocidade, :
Estamos quase lá!
Passo 7
E para sabermos a direção, calculamos:
Ou seja, abaixo da horizontal.
A velocidade da bola quando retorna ao nível em que saiu do bastão é de 30,0 m/s e é direcionada a um ângulo de abaixo da horizontal.
E aí! o que achou? Responde Aí!
Resposta
- e abaixo da horizontal