Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 12.Questões Conceituais - Ex. 2

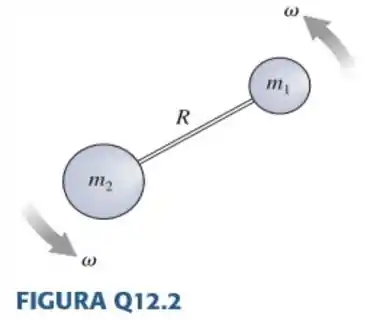
2. Se a velocidade angular ω se mantiver constante, em que fator deve R variar a fim de dobrar a energia cinética de rotação do haltere da FIGURA Q12.2?

Passo 1

Bom! Nós sabemos que a energia cinética de rotação é dada por...

K r o t a ç ã o = I ω 2 2

Agora uma coisa que nós não sabemos é onde está o centro de massa dessa partícula. De qualquer forma, podemos determinar a energia cinética para o momento inicial como sendo igual

K a n t e s = I 1 ω 2 2 + I 2 ω 2 2

Onde I 1 é o momento de inércia da massa 1 e I 2 é o momento de inércia da massa 2 . A massa 1 está a uma distância L 1 do centro de rotação e a massa 2 está a uma distância L 2 da massa 2 .

De modo que...

L 1 + L 2 = R

E ficamos então com...

K a n t e s = m 1 L 1 2 ω 2 2 + m 2 L 2 2 ω 2 2

K a n t e s = ω 2 2 ( m 1 L 1 2 + m 2 L 2 2 )

Passo 2

Imagina agora multiplicarmos L 1 por 2 e L 2 por 2 e substituir na expressão da energia cinética.

K d e p o i s = m 1 ( 2 L 1 ) 2 ω 2 2 + m 2 ( 2 L 2 ) 2 ω 2 2

K d e p o i s = ω 2 2 ( 2 m 1 L 1 2 + 2 m 2 L 2 2 )

K d e p o i s = ω 2 ( m 1 L 1 2 + m 2 L 2 2 )

Obteremos assim, o dobro do valor anterior. Como L 1 e L 2 foram multiplicados por 2 , o valor do novo raio será...

R n o v o = 2 ( L 1 + L 2 )

R n o v o = 2 R

Sendo assim, R deve ser multiplicado por 2 a fim de dobrar a energia cinética rotacional.

Resposta

R   d e v e   s e r   m u l t i p l i c a d o   p o r   2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Terra, que não é uma esfera uniforme, possui momento de inércia igual a 0,3308 M R 2 em relação a um eixo ligando o pólo norte ao pólo sul. O tempo para a Terra completar um giro é igual a 86164 s.
Ao reprojetar o motor de um foguete, você deseja reduzir seu peso substituindo uma peça esférica maciça por uma casca esférica oca do mesmo tamanho. As peças giram em torno de umeixo que passa pelo se
Exatamente uma volta de uma corda flexível de massa m é enrolada na periferia de um cilindro uniforme maciço de massa M e raio R. O cilindro gira sem atrito em torno de um eixo horizontal ao longo do
Uma placa de sinalização em metal de uma concessionária de automóveis é um tri��ngulo retângulo delgado com base de comprimento b e altura h. A placa possui massa M. a) Qualé o momento de inércia da p
Uma régua de um metro e massa igual a 0,160 kg possui um pivô em uma de suas extremidades de modo que ela pode girar sem atrito em torno de um eixo horizontal. A régua é mantida em uma posição horizon