Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 8.Problemas Adicionais - Ex. 118

Com o arranjo de forças do Problema 81, uma partícula de 2,00   k g é liberada em x   =   5,00   m , com uma velocidade de 3,45   m / s , no sentido negativo do eixo   x . (a) Se a partícula pode chegar ao ponto x   =   0   m , qual é a velocidade da partícula nesse ponto; se não pode, qual é o ponto de retorno? Suponha que a partícula se move no sentido positivo de x quando é liberada em x   =   5,00   m com uma velocidade de 3,45   m / s . (b) Se a partícula pode chegar ao ponto x   =   13,0   m , qual é a velocidade da partícula nesse ponto; se não pode, qual é o ponto de retorno?

Figura 8-64 Problema 82.

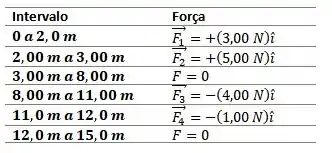
Passo 1

a) A energia cinética em x = 5,0   m é

K 5 = 1 2 m v 2

Para m = 2,0   k g e v = 3,45   m / s

K 5 = 2.3,45 2 2

K 5 = 11,9025   J

Como para atingir o ponto x = 0 é necessário apenas 11   J , temos que a energia cinética nesse ponto será

K 2 = U 0 + K 0

K 0 = K 2 - U 0 = 11,9025 - 11 = 0,9025   J

Logo, a velocidade será

K 0 = 1 2 m v 2

v = 2 K 0 m = 2.0,9025 2

v = 0,95   m / s

Passo 2

b) A energia total no início do movimento é K 5 = 11,9025   J e será toda transformada em energia potencial a partir de x = 8   m , logo

K f - K i = W

Com K f = 0 , K i = K 8 = K 5 e W = F 3 . x

F 3 x = - 11,9025

- 4 x = - 11,9025

x ≈ 2,98   m

Logo, depois de x = 2,98   m depois de passar por x = 8   m , toda a energia cinética foi convertida em energia potencial. Dessa forma

x f = 8 + 2,98 = 10,98

x f ≈ 11   m

Resposta

a) A partícula chega ao ponto e sua velocidade é v = 0,95   m / s

b) A partícula não chega ao ponto e seu ponto de retorno é em x f ≈ 11   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bloco de madeira com massa igual a 1,50 kg é colocado contra uma mola comprimida na base de um plano inclinado de 30,0° (ponto A). Quando a mola é libertada, projeta o bloco para cima do plano incl
Os companheiros do grêmio estudantil Iota Eta Pi construíram uma plataforma apoiada nos quatro cantos sobre molas verticais no porão da casa da agremiação. Um bravo companheiro do grêmio usando um cap
Uma mola cuja constante é igual a 40,0N / m e comprimento de 0,60m , está presa a um bloco de 0,500k g apoiado em repouso sobre uma mesa de ar horizontal sem atrito, sendo A a posição inicial do ponto
Um bloco de 3,0k g está conectado a duas molas ideais horizontais com constantes de força k 1 = 25,0N / c m e k 2 = 20,0 N / c m (Figura 7.42). O sistema está inicialmente em equilíbriosobre uma super
Um pacote de 2,0 kg inicialmente em repouso é abandonado sobre um plano inclinado de 53,1°, a uma distância de 4,0 m de uma mola com constante de 120 N/m presa à base do um plano (Figura 7.43). Os coe