Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 7.Problemas - Ex. 73

Um bloco de madeira com massa igual a 1,50 kg é colocado contra uma mola comprimida na base de um plano inclinado de 30,0° (ponto A). Quando a mola é libertada, projeta o bloco para cima do plano inclinado. No ponto B situado a uma distância de 6,0 m acima do ponto A, o bloco está subindo o plano inclinado com velocidade de 7,0 m/s e não está mais em contato com a mola. O coeficiente de atrito cinético entre o bloco e o plano inclinado é . A massa da mola é desprezível. Calcule a energia potencial que foi inicialmente armazenada na mola.

Passo 1

Olá, meu querido amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.

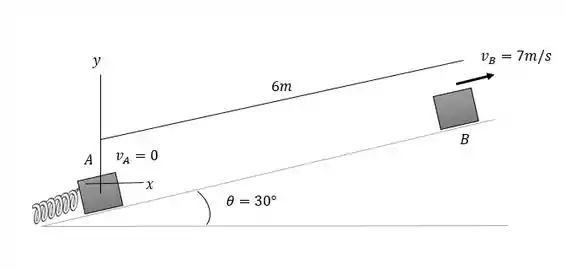
A figura abaixo nos ajuda a visualizar a situação. Temos uma situação onde a energia potencial elástica joga um bloco em um plano inclinado, parte da energia é utilizada para gerar energia cinética para o bloco, outra parte é perdida para o trabalho da força de atrito e uma parte energia potencial gravitacional.

Passo 2

Vamos aplicar ao movimento do bloco a equação:

variação da energia cinética

variação da energia potencial

E descrever o momento de A para B:

A força normal é:

Assim, temos que o atrito cinético é dado por:

Temos que:

E

E sabemos que:

Passo 3

O trabalho é feito pela gravidade, pela força da mola e pelo atrito, de modo que:

E

Passo 4

Para calcularmos a energia potencial que foi inicialmente armazenada na mola fazemos:

, assim,

E desde que seja nula, .

Agora fazemos para:

Passo 5

Então, calculando para:

Passo 6

E então temo que:

E isso implica que:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula de 3,0 kg, que se move ao longo do eixo x, tem uma velocidade de +2,0 m/s quando passa pela origem. Ela está sujeita a uma força única, F x , que varia com a posição como mostrada na fig

Uma partícula de massa m move-se em uma dimensão com energia potencial U(x) representada pela curva da Fig.( as beiradas abruptas são idealizações de um potencial rapidamente variável. Inicialmente a

Uma partícula move-se ao longo da direção x sob o efeito de uma força F x =- k x + K x 2 , onde k = 200N / me K = 300N / m 2 . a) Calcule a energia potencial U(x) da partícula, tomando U(0) = 0, e faç

Um oscilador harmônico tridimensional isotrópico é definido como uma partícula que se move sob a ação de forças associadas à energia potencial U x , y , z = 1 2 k ( x 2 + y 2 + z 2 ) Onde k é uma cons

Uma partícula está confinada a mover-se no semi-espaço z ≥0 , sob a ação de forças conservativas, de energia potencial U x , y , z = F 0 z + 1 2 k x 2 + y 2 , onde F 0ek são positivas. a) Calcule as c