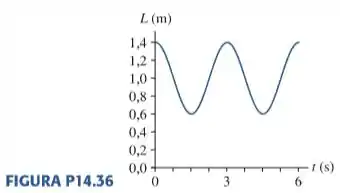
Astronautas no espaço não conseguem se pesar ficando em pé sobre uma balança comum de banheiro. Em vez disso, eles determinam sua massa oscilando presos a uma grande mola. Suponha que uma astronauta prenda a extremidade de uma grande mola a seu cinto e a outra extremidade a um gancho fixado no interior da nave espacial. Outro astronauta a puxa na direção oposta ao gancho e a solta. O comprimento da mola em função do tempo é mostrado na FIGURA P14.36.

a. Qual é a massa da astronauta se a constante elástica for de ?

b. Qual é a sua velocidade quando o comprimento da mola for de ?

Com isso, podemos determinar qual é a amplitude do movimento, basta pegarmos o máximo (ou o mínimo) e subtrair o valor da posição do ponto de equilíbrio:

Esse é o maior valor de deslocamento em relação ao equilíbrio que a mola pode chegar, que é a amplitude

Outra informação que podemos tirar do gráfico é o período, de até , a mola foi de , passou por todos os valores possíveis e chegou em de novo, isso significa que o período é de:

Com ele e a amplitude, podemos calcular a velocidade máxima do astronauta:

Substituindo:

E usando a equação de conservação de energia, podemos encontrar a massa do astronauta:

A energia mecânica total é toda convertida em energia cinética quando o astronauta está no ponto de equilíbrio.

Agora basta isolarmos :

Substituindo os valores:

Para a letra (b), basta usarmos a equação de energia novamente, mas nesse caso, como a mola está numa posição em que ela não está completamente esticada ou na posição de equilíbrio, a energia mecânica total é dada pela soma da energia cinética com a energia potencial elástica:

Simplificando:

Como é a variação de comprimento da mola em relação ao equilíbrio que está em :

Nossa equação fica:

Agora a gente isola :

E substitui todos os valores que a gente calculou ou o enunciado deu: