Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 40.Problemas adicionais - Ex. 65
Os átomos de sódio excitados emitem duas linhas espectrais muito próximas (o chamado dubleto do sódio; veja fig 40-27) com comprimentos de onda de e .
- Qual é a diferença de energia entre os dois níveis superiores ()
-
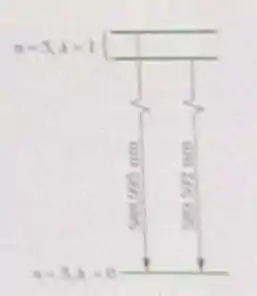A diferença de energia do item a) se deve ao fato de que o momento magnético de spin do elétron pode estar orientado paralela ou antiparalelamente ao campo magnético associado ao movimento orbital do elétron. Usa o resultado do item a) para calcular o módulo desse campo magnético interno.
Passo 1
Letra a)
A energia associada a cada nível é dada por:
E a energia de trasição entre dois níveis pode ser dada em função do comprimento de onda:
Como temos e a diferença de energia é:
Passo 2
Letra b)
A energia associada ao campo magnético é , então daqui e juntando o resultado da energia do item anterior, podemos calcular :
Resposta
Exercícios de Livros Relacionados
Existe uma probabilidade finita, embora muito pequena, de que um elétron de um átomo seja encontrado no interior do núcleo. Na verdade, alguns núcleos instáveis usam essa presença ocasional do elétron
As funções de onda normalizadas para uma partícula confinada a se mover num circulo são: ψ ϕ = 1 2 π 1 2 e - i m ϕ , onde m = 0 , ± 1 , ± 2 , ± 3 , …, e 0 ≤ ϕ ≤ 2 π . Determine ϕ .
Determine quais, entre as seguintes funções, são autofunções do operador inversão i ^ (operador que transforma x → - x ): (a) x 3 - k x ; (b) cos k x ; (c) x 2 + 3 x - 1 .Quando for apropriado, dete
Quais, dentre ad funções do Problema 8.15, são (a) também autofunções do operador ( d 2 / d x 2 ) e (b) exclusivamente autofunções de ( d 2 / d x 2 ) ? Dê os autovalores quando for apropriado.
Uma partícula está num estado descrito pela função de onda Ψ = cos χ e i k x + sin χ e - i k x Onde χ c h i é um parâmetro. Qaul é a probabilidade de a partícula ter o momento linear (a) - k ℏ ; (