Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 3.3 - Ex. 12
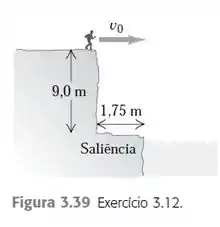
Uma ousada nadadora salta correndo 510 N e horizontalmente de um rochedo para um
mergulho, conforme a Figura 3.39. Qual deve ser sua velocidade mínima quando salta do topo do rochedo, de modo que ela consiga ultrapassar uma saliência no pé do rochedo, com
largura de 1,75 m e 9,0 m abaixo do topo?
Passo 1
Fala aí! tudo certinho?
Nesse problema temos um movimento balístico de uma pessoa que salta a de altura e precisa se mover horizontalmente antes de chegar ao solo.
A partir daí queremos saber qual deve ser a velocidade inicial mínima para que isso ocorra.
Parece complicado?
Primeiro passo é analisar o que está acontecendo na questão:
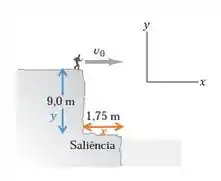
Vamos tomar como:
No temos um movimento uniforme (MU) com:
No : temos um movimento em queda livre com:
Veja só!
Passo 2
Agora precisamos encontrar o tempo que leva para cair , a partir da equação:
Substituindo os valores dados no problema, temos
Tranquilo até aqui? 😬
Passo 3
Agora que já sabemos o tempo, , podemos encontrar a velocidade necessária, , que ele leva para percorrer durante o período.
Se ela aumenta sua velocidade inicial, ainda leva para atingir o nível da borda, mas “viajou” horizontalmente além de .
E aí! entendeu tudo? Responde Aí! 😁
