Um helicóptero militar em missão de treinamento voa horizontalmente com velocidade de e acidentalmente deixa cair uma bomba (felizmente não ativa) de uma altura de . Despreze a resistência do ar. a) Quanto tempo a bomba leva para atingir o solo? b) Qual a distância horizontal percorrida pela bomba durante a queda? c) Ache os componentes da velocidade na direção horizontal e na vertical imediatamente antes de a bomba atingir o solo. d) Faça diagramas , , e para o movimento da bomba. e) Mantida constante a velocidade do helicóptero, onde estaria ele no momento em que a bomba atingisse o solo?
Passo 1
Belezoca galerinha bonita! Repara que nessa questão temos uma bomba que se solta de um helicóptero que possui um velocidade horizontal, deste modo, a velocidade inicial da bomba será a mesma que a do helicóptero.
Podemos esboçar a situação descrita no enunciado para compreendermos melhor:
A bomba se move em movimento de projétil e o tempo de queda determinará o seu tempo no ar.
Vamos tomar o movimento da bomba caindo como .
Passo 2
- Como estamos despresando a resistência do ar, a bomba se encontra em queda livre, então a sua aceleração é a a aceleração gravitacional, já conhecida por nós:
- Para sabermos a distancia horizontal que a bomba alcança, temos que:
- Bom, nós temos que: na direção de .
- Os diagramas , , e se dão por:
- O helicóptero e a bomba sempre têm o mesmo componente em de velocidade e posição, então o helicóptero estaria a 300m diretamente acima da bomba no impacto.
Pelo enunciado temos que a velocidade do helicptero é: , e essa é a velocidade inicial da bomba também.
Temos que a bomba parte do repouso, em relação ao helicóptero, então, .
Além do mais, sabemos que a altura é: .
Agora podemos encontrar o tempo de queda da bomba, a partir da equação:
diferença de altura
velocidade inicial
tempo
gravidade
Logo
Algo importante a se comentar é independência do movimento, o movimento horizontal e o movimento vertical da bomba são independentes e esse tempo pode ser utilizado para encontrar o deslocamento na horizontal da bomba ou do helicóptero.
Passo 3
Agora, temos os seguintes dados:
Então, temos que:
Passo 4
Então, vamos utilizar a equação para achar a componente da velocidade na vertical.
Portanto,
Passo 5
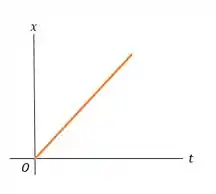
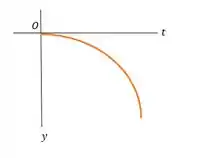
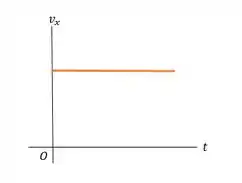
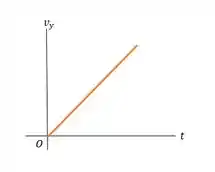
Passo 6
Resposta
-
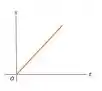

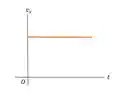

- Acima da bomba.