Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 3.3 - Ex. 27
Um avião voa a uma velocidade de , a um ângulo de acima da horizontal. Quando está a diretamente sobre um cachorro parado no nível do solo, uma mala cai do compartimento de bagagens. A que distância do cachorro a mala vai cair? Despreze a resistência do ar.
Passo 1
Oi, galerinha! Tudo bom?
Na situação descrita, a mala cai do avião, deste modo ela possui uma velocidade inicial horizontal igual a do avião. Ao cair, ela fará um movimento obliquo até o solo. Vamos representar a situação:
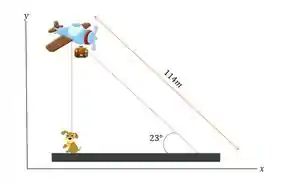
Note que a distância entre o avião e o cachorro é perpendicular ao solo, portanto, temos um triangulo retângulo representado na situação.
Vamos tomar como sendo para cima, então sobre a aceleração, temos apenas a aceleração da gravidade agindo sobre a mala, então em cada eixo:
Veja só!
Passo 2
Nós vamos utilizar o movimento vertical para encontrar o tempo que a mala leva para chegar ao chão. A velocidade pode ser decomposta em duas componentes:
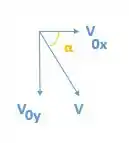
Sendo
Temos que:
Então vamos utilizar a equação para encontrar o tempo necessário para a bagagem chegar ao chão:
Substituindo os valores que já conhecemos:
Vamos multiplicar os dois lados por 2:
Dividindo os dois lados por -9,8:
Temos que resolver essa equação dos segundo grau e acharemos o tempo:
Como só podemos ter um valor de tempo positivo:
Tranquilo até aqui?
Passo 3
A distância que a mala percorre horizontalmente é dada por:
Como já falamos como essa velocidade é composta, podemos substituir a velocidade no eixo por:
Substituindo os valores que já conhecemos:
E aí! entendeu tudo? Responde Aí! 😊
