Pelé chuta uma bola de futebol com velocidade inicial tal que o componente vertical é igual a 16,0 m/s e o componente horizontal é igual a 20,0 m/s. Despreze a resistência do ar. a) Quanto tempo a bola leva para atingir a altura máxima de sua trajetória? b) Qual a altura desse ponto? c) Quanto tempo a bola leva (desde o momento do chute inicial) até o instante em que ela
retorna ao mesmo nível inicial? Qual é a relação entre esse tempo e o calculado no item (a)? d) Que distância horizontal ela percorreu durante esse tempo? e) Faça diagramas , , e para o movimento.
Passo 1
E aí, galerinha!

Nesse problema temos uma situação onde e Pelé chuta uma bola onde a velocidade inicial dela é dada por
A partir daí queremos saber qual é o tempo que a bola leva até atingir sua altura máxima, a altura máxima, o tempo para que ela volte à altura inicial e a distancia horizontal percorrida...
Parece complicado?
Depois que a bola é chutada ela entrar em movimento de projetil, então nós temos que trabalhar suas componentes de e separadamente.
Vamos tomar, na vertical, como para cima.
A aceleração na horizontal, é: .
E a aceleração na vertical, é: .
No ponto mais alto da trajetória da bola, a velocidade é: .
Veja só!
Passo 2
Então, para calcular o tempo, vamos utilizar a seguinte equação:
Tranquilo até aqui?
Passo 3
Para encontrarmos a altura, não dependemos do tempo, , então podemos utilizar a equação de Torricelli:
Vamos tomar . E como queremos calcular a altura, devemos utilizar o , desta forma:
Temos que: .
Então:
Bacana, não é?
Passo 4
O tempo total é o dobro do tempo que encontramos no item (a), pois consideramos que o tempo de subida é o mesmo que o tempo de descida, então temos que:
Estamos quase lá!
Passo 5
Para sabermos o deslocamento total temos que:
Então,
Show, né?
Passo 6
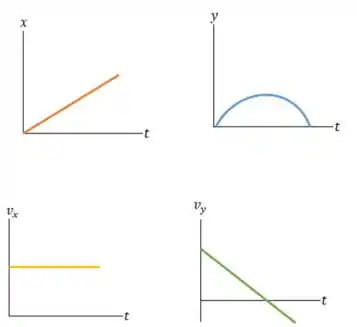
E podemos concluir que nossos gráficos ficam do seguinte formato:
E aí! entendeu tudo? Responde Aí!
Resposta
- Gráficos: