Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 92

Um avião está voando em um círculo horizontal a uma rapidez de 480   k m / h . O avião é inclinado para essa curva, de forma que suas asas formam um ângulo de 40 ° com a horizontal. Assuma que uma força de empuxo agindo perpendicularmente às asas age sobre a aeronave conforme ela se move pelo ar. Qual é o raio do círculo em que o avião está voando?

Passo 1

Vamos começar representando as forças que agem sobre o avião:

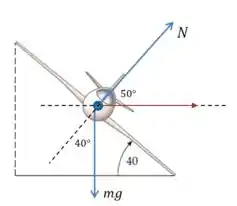
A seta vermelha no desenho indica a direção da resultante centrípeta. A única contribuição nessa direção vem de uma componente da força N de empuxo:

N cos ⁡ 50 ° = m v 2 r

E como nosso objetivo é calcular o raio r :

r = m v 2 N cos ⁡ 50 °

Fica faltando apenas calcular o módulo da força N .

Passo 2

Se o avião está voando em um círculo horizontal, as forças na direção vertical precisam estar em equilíbrio, ou seja:

N sen ⁡ 50 ° = m g

N = m g sen ⁡ 50 °

Substituindo isso na equação de cima:

r = m v 2 N cos ⁡ 50 ° = v 2 g tan ⁡ 50 °

A rapidez é v = 480   k m / h = 133   m / s :

r = 133 2 9,81 tan ⁡ 50 °

r ≅ 2,2   k m

Resposta

O avião descreve um círculo de raio aproximadamente igual a 2,2   k m .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bloco de 60 kg desliza sobre o topo de um bloco de 100 kg. O bloco de 60 kg tem uma aceleração de 3,0m / s 2 enquanto uma força horizontal de 320 N é aplicada a ele, como mostra a figura abaixo. Nã
Uma massa de 100 kg é puxada sobre uma superfície sem atrito por uma força horizontal F → , de forma que sua aceleração é a 1 = 6,00m / s 2 (figura abaixo). Uma massa de 20 kg desliza sobre o topo da
O coeficiente de atrito estático entre um pneu de borracha e a superfície de uma estrada é 0,85. Qual é a aceleração máxima de um caminhão de 1000 kg de tração nas quatro rodas, se a estrada forma um
Responda às questões do Problema 54, mas para uma força F → que empurra o bloco a um ângulo θ abaixo da horizontal.
Considere o bloco da figura abaixo. Mostre que, em geral, os seguintes resultados valem para um bloco de massa m que está sobre uma superfície horizontal de coeficiente de atrito estático μ e . (a) Se