Um balanço improvisado foi construído amarrando as duas extremidades de uma corda no galho de uma árvore. Uma criança está sentada no meio com os dois trechos da corda na vertical, quando o pai da criança a empurra com uma força horizontal, deslocando-a para um lado. Imediatamente antes de a criança ser liberada a partir do repouso, a corda faz um ângulo de com a vertical e a tensão da corda é . (a) Quanto pesa a criança? (b) Qual é o módulo da força (horizontal) que o pai exerce sobre a criança imediatamente antes de liberá-la? (c) Se a força máxima que o pai pode exercer sobre a criança é , qual é o maior ângulo com a vertical que a corda pode fazer enquanto o pai empurra horizontalmente a criança?
Passo 1
Vamos começar com um desenho da situação. Nesse desenho, já vamos decompor a força de tração na corda em duas componentes: e :
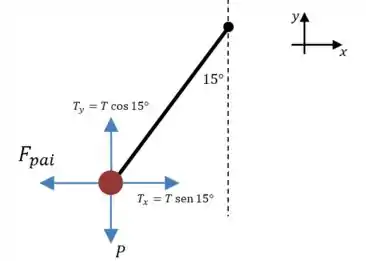
E agora nós podemos escrever as equações de equilíbrio desse sistema em cada uma das direções:
Passo 2
(a) Nosso primeiro objetivo é encontrar o peso da criança, sabendo que o ângulo de está associado a uma tensão de na corda. Então, se substituirmos na segunda equação do nosso sistema:
Passo 3
(b) Agora que conhecemos e , queremos calcular o módulo da força que o pai exerce sobre a criança antes de liberá-la. Vamos olhar de novo para o nosso sistema:
Podemos dividir a primeira equação pela segunda para encontrar o seguinte:
Passo 4
(c) Finalmente ,queremos saber qual seria o ângulo formado pela corda com a horizontal no caso em que .
Então vamos reescrever nosso sistema colocando no lugar dos , e substituindo os outros valores numéricos:
Precisamos eliminar a variável , então vamos dividir a primeira equação pela segunda:
Resposta
(a) .
(b) .
(c) .