Um balanço improvisado foi construído fazendo uma alça em uma das pontas de uma corda e amarrando a outra ponta no galho de uma árvore. Uma criança está sentada na alça, com a corda na vertical, quando o pai da criança a empurra com uma força horizontal, deslocando-a para um lado. Imediatamente antes de a criança ser liberada a partir do repouso, a corda faz um ângulo de com a vertical, e a traçaõ da corda é de . (a) Quanto pesa a criança? (b) Qual é o módulo da força (horizontal) que o pai está exercendo sobre a criança, imediatamente antes de liberá-la? (c) Se a força máxima que o pai pode exercer sobre a criança é , qual é o maior ângulo com a vertical que a corda pode fazer enquanto o pai empurra horizontalmente a criança?
Passo 1
Vamos fazer um desenho para representar essa situação:
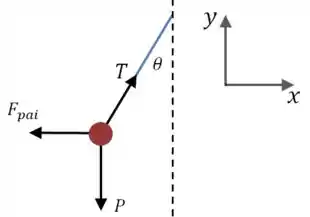
Para que a criança permaneça em repouso, precisamos ter equilíbrio das forças nas duas direções:
Onde e são as componentes da força nas direções horizontal e vertical:
Então ficamos com o seguinte sistema:
Passo 2
(a) Nosso primeiro objetivo é encontrar o peso da criança, sabendo que ocorre equilíbrio quando o ângulo mede e a tração na corda é .
Vamos olhar para a primeira equação do nosso sistema:
Passo 3
(b) E para encontrar o módulo da força exercida pelo pai nesse mesmo instante, só precisamos olhar para a segunda equação do sistema:
Passo 4
(c) Agora queremos calcular qual é o ângulo máximo que a corda pode formar com a vertical, sabendo que o pai só pode exercer uma força de até .
Vamos olhar mais uma vez para o nosso sistema, já substituindo o valor do peso :
Não sabemos qual será a tração da corda quando o ângulo for máximo, então temos que eliminar de alguma forma. Vamos dividir a segunda equação pela primeira:
Então, quando a força for máxima, o ângulo máximo será:
Resposta
(a) O peso da criança é de .
(b) A força exercida pelo pai é de .
(c) O ângulo máximo é de .