Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 8.Problemas - Ex. 10
Uma barra cilíndrica homogênea de 3m de comprimento é dobrada duas vezes em um ângulo reto, a intervalos de 1m de modo a formar três arestas consecutivas de um cubo(Fig.). Ache as coordenadas do centro de massa da barra, no sistema de coordenadas da figura.
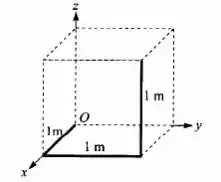
Passo 1
Aqui isolando cada barra o seu centro de massa individual é exatamente em seu centro, então vamos trabalhar com os centros das barras
- Barra no eixo
- Barra no eixo
- Barra no eixo
Agora vamos calcular as coordenadas do centro de massa total usando esses valores, saca só
Resposta
Exercícios de Livros Relacionados
CALC Use os métodos do Problema desafiador 8.104 para determinar as coordenadas x e y do centro de massa de uma placa metálica semicircular com densidade uniforme e espessura t. Chame de a o raio da p
Um eixo uniforme possui 2,00 m de comprimento e massa de 1,80 kg. Um grampo de 2,4 kg é preso ao eixo. A que distância o centro de gravidade deverá estar do grampo a partir da extremidade esquerda do
Os amigos Beto e Ernesto estão parados em extremidades opostas de um tronco uniforme flutuando em um lago. O tronco tem 3,0m de extensão e massa de 20,0k g . Beto tem massa de 30,0k g e Ernesto, de 40
Quais são (a) a coordenada x e (b) a coordenada y do centro de massa da placa homogênea da Fig. 9-38 se L = 5,0c m ?
Determine a posição do centro de massa do sistema constituído pelo Sol e por Júpiter. (Como a massa de Júpiter é muito maior do que as massas dos demais planetas, esta resposta fornece essencialmente