Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 23.Exercícios e Problemas - Ex. 13
a) Uma barra de comprimento gira com velocidade angular no plano horizontal em torno de um eixo passando por uma das suas extremidades. Em toda a região varrida pela barra existe um campo magnético homogêneo vertical de intensidade . Calcule a fem induzida entre as extremidades da barra.
b) Refaça o cálculo para o caso em que o eixo passe pelo meio da barra.
Passo 1
Fala pessoal, tudo tranquilo?
Para entender bem esse problema aconselho você a dar uma olhadinha na seção 23.7 do livro, que discute situações em que aparece uma fem induzida sem haver necessariamente um fluxo magnético ou coisa do tipo.
A expressão que vamos utilizar nesse problema é dada na equação 23.37. A fem induzida gerada em um corpo carregado em movimento é
Vamos considerar a situação da barra girando:
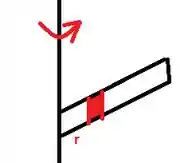
A velocidade de um pedaço da barra com comprimento a uma distância do eixo de rotação é
Como o campo magnético está na direção (direção do eixo) temos
Assim,
Portanto, basta integrar entre os limites de integração corretos para achar a fem induzida!
Passo 2
No item (a) temos exatamente a situação da figura, de modo que a integral vai de até para acharmos a fem entre os extremos da barra:
Daí é só substituir os valores:
Fazendo as continhas:
No item (b) o eixo de rotação está no centro da barra e queremos a fem entre as extremidades. É fácil perceber que os limites de integração serão iguais a de modo que a fem será nula:
Eu sei que o exercício parece estranho pois não falamos de fluxo magnético para achar a fem induzida, mas isso é sim possível, como foi discutido no libro!