Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.5 - Ex. 34
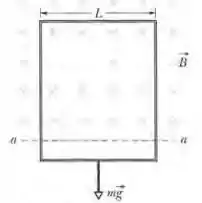
Na Fig. 30-58, uma espira retangular muito longa, de largura , resistência e massa , está inicialmente suspensa na presença de um campo magnético horizontal uniforme orientado para dentro do papel, que existe apenas na região acima da reta . Deixa-se cair a espira, que acelera sob ação da gravidade até atingir uma velocidade terminal . Escreva uma expressão para , ignorando a resistência do ar.
Passo 1
Fala aí, pessoal! 😇
O problema fala de uma espira que cai sob ação da gravida numa região em que há um campo magnético. Como a área sob a qual o campo age varia com o tempo conforme a espira cai, a variação do fluxo induz a passagem de uma corrente elétrica na espira. Essa corrente sentirá uma força magnética para cima que vai se opor à gravidade. Em algum instante, será atingida uma velocidade terminal, que ocorre quando
Temos que saber qual é a velocidade de queda da espira quando isso ocorrer!
Veja só! 😊
Passo 2
O fluxo magnético sobre a espira será
Assim, a derivada com relação ao tempo será dada por
Assim, em módulo, a fem induzida será dada por
Por outro lado, pela lei de Ohm:
Bacana, não é? 😉
Passo 3
Desta forma, na situação limite da velocidade terminal:
Portanto
E aí! entendeu tudo? Responde Aí! 👀
