Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 11.1 - Ex. 105

Uma barra fina e homogênea de 20   k g , com 5,0   m de comprimento, é dobrada em um semicírculo. Qual é a força gravitacional exercida pela barra sobre uma massa pontual de 0,10   k g localizada no centro da curvatura do arco circular?

Passo 1

Vamos começar desenhando o que temos. A barra que o problema descreve é a seguinte:

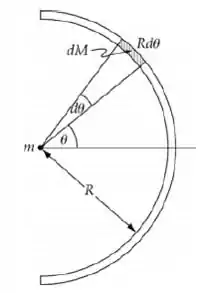
Como temos um semicírculo homogêneo, podemos afirmar que temos um elemento de comprimento R d θ = L π d θ que tem massa d M = M π d θ . Perceba que como é um semicírculo, dividimos as duas grandezas ( R e M ) por π . Pela simetria do problema, podemos afirmar que F y = 0 . Vamos usar a estratégia de primeiro achar d F x em função de θ e então integrar de - π 2 a π 2 .

Passo 2

Podemos expressar d F x desse jeito:

d F x = G m d M R 2 = G M m π L π 2 d θ cos ⁡ θ

Agora podemos integrar os dois lados da equação! Integrando de π 2 a π 2 :

F x = ∫ - π 2 π 2 G M m π L π 2 d θ cos ⁡ θ

Agora vamos jogar tudo que seja constante pra fora da integral:

F x = π G M m L 2 ∫ - π 2 π 2 cos ⁡ θ d θ

Passo 3

Calculando essa integral:

∫ - π 2 π 2 cos ⁡ θ d θ = [ - sin ⁡ θ ] - π 2 π 2 = 1 + 1 = 2

Agora substituindo o valor dela na equação de F x :

F x = 2 π G M m L 2

Agora é só substituir os valores e GG!

F x = 2 π 6.67 ∙ 10 - 11   m 3 k g - 1 s - 2 20   k g 0.10   k g 5.0   m 2 = 34   p N

Cabôsse! Esse é o nosso resultado.

Resposta

34   p N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas esferas maciças muito afastadas, E 1 e E 2 , têm o mesmo raio R e a mesma massa M . A esfera E 1 é homogênea, enquanto a massa específica de E 2 é dada por ρ r = C / r , onde r é a distância ao s
Uma casca esférica fina e homogênea tem 2,0 m de raio e 300 k g de massa, e seu centro está localizado na origem de um sistema de coordenadas. Outra casca esférica fina e homogênea, com 1,00 m de raio
Suponha que a Terra seja uma esfera homogênea não girante. Como prêmio por terem recebido a maior nota de laboratório, seu professor de física escolhe sua equipe de laboratório para participar de um e
Suponha que você esteja de pé sobre uma balança de mola em um elevador que está descendo, com rapidez constante, o túnel de entrada de uma mina localizada no equador. Trate a Terra como uma esfera hom
Duas esferas maciças e homogêneas muito afastadas, E 1 e E 2 , têm massas iguais mas raios diferentes, R 1 e R 2 . Se a intensidade do campo gravitacional na superfície de E 1 é g 1 , qual é a intensi