Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 6.Problemas - Ex. 55

Uma barra fina e uniforme de 12,0   k g e 2,0   m de comprimento gira de maneira uniforme em torno de um pivô em uma das suas extremidades, fazendo 5,0 revoluções completas a cada 3,0   s e g u n d o s .

Qual é a energia cinética dessa barra? (Sugestão: a velocidade varia em diferentes pontos da barra. Segmente a barra em partes infinitesimais de massa d m e some a energia cinética de todos esses segmentos.)

Passo 1

Opa, bora resolver esse problema! Temos uma barra fazendo movimento circular assim:

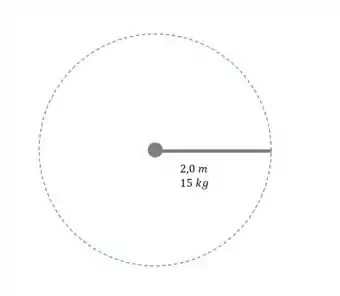
Imagina que esse esqueminha é uma foto tirada por cima da barra. Em 3 segundos a barra faz 5 voltas completas em torno do centro. Sabendo disso demos responder a qual é a energia cinética da barra!

Vamos dizer que T é o tempo de uma revolução e que v é a velocidade linear, então:

v = 2 π x T

E a barra é homogênea, então:

M L = d m d x

d m = M L d x

Passo 2

A energia cinética infinitesimal vai ser:

d K = 1 2 v 2   d m

E podemos substituir v e d m :

d K = 1 2 2 π x T 2 M L d x

E os dados que o problema nos trás são:

M = 12 k g

L = 2 m

T = 3 5 s

Agora é só integrar dos dois lados!

Passo 3

Integrando a expressão pra energia cinética:

K = ∫ 0 L 1 2 2 π x T 2 M L d x

Tiramos as constantes da integral:

K = 1 2 4 π 2 T 2 M L ∫ 0 L x 2 d x

Agora é só integrar e substituir os limites de integração:

K = 1 2 4 π 2 T 2 M L . x 3 3 0 L = 1 2 4 π 2 T 2 M L L 3 3

K = 1 2 4 π 2 T 2 M L 2 3

Agora vamos substituir os valores:

K = 2 π 2 . 12.2 2 3 . 3 5 2 = 877 J

Prontiho!

Resposta

877 J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma conta com uma massa de 1,8× 10 - 2k g está se movendo no sentido positivo do eixo x . A partir do instante t = 0 , no qual a conta está passando pela posição x = 0 com uma velocidade de 12m / s ,
Um próton (massa m = 1,67 × 10 - 27k g ) está sendo acelerado em linha reta a 3,6 × 10 15m / s 2 em um acelerador de partículas. Se o próton tem uma velocidade inicial de 2,4 × 10 7m / s e se desloca
Em 10 de agosto de 1972, um grande meteorito atravessou a atmosfera sobre o oeste dos Estados Unidos e Canadá como uma pedra que ricocheteira na água. A bola de fogo resultante foi tão forte que pôde
Em uma corrida, um pai tem metade da energia cinética do filho, que tem metade da massa do pai. Aumentando a velocidade em 1,0m / s , o pai passa a ter a mesma energia cinética do filho. Qual é a velo
O motor de um carro de massa m fornece uma potência constante P para as rodas, para acelerar o carro. Despreze a resistência do ar e o atrito de rolamento. O carro está inicialmente em repouso. a) Mos