Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 12.Problemas - Ex. 84
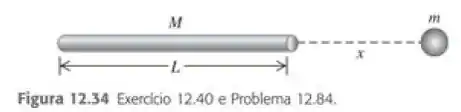
Uma barra uniforme deslgada possui comprimento e massa . Calcule o modulo da força gravitacional que a barra exerce sobre uma partícula de massa situada ao longo do eixo da barra a uma distancia de uma de suas extremidades (Figura 12.34). Mostre que o seu resultado se reduz ao esperado quando for muito maior do que .
Passo 1
Bom, galera, aqui vamos usar a equação da lei da gravitação
para a força entre um pequeno segmento da haste e a partícula. Integraremos sobre o comprimento da haste para encontrar a força total.
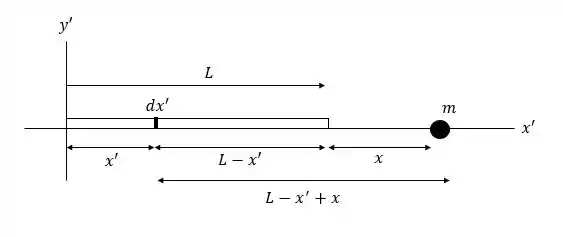
Vamos usar um sistema de coordenadas com a origem na extremidade esquerda da haste e o eixo ao longo da haste, como mostrado na ilustração abaixo. Dividiremos a haste em pequenos segmentos de comprimento . (Vamos usar para a coordenada para não
confundir com a distância do final da haste até a partícula.)
Passo 2
A massa de cada segmento é
Cada segmento é uma distância da massa , então a força na partícula devido a um segmento é
Passo 3
Integrando, temos que:
Passo 4
Para esse resultado se torna , o mesmo que para um par de massas pontuais.