Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 12.Problemas - Ex. 83
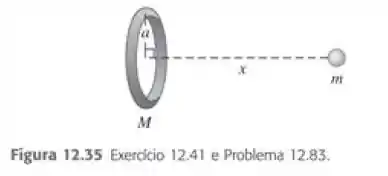
Um corpo com forma de anel fino possui raio e massa . Uma esfera uniforme de raio e massa é colocada com seu centro situado a uma distancia à direita do centro do anel, sobre a linha que une os centros perpendicular ao plano do anel (Figura 12.35). Qual é a força gravitacional que a esfera exerce sobre o corpo em forma de anel? Mostre que o seu resultado se reduz ao esperado quando for muito maior do que .
Passo 1
O cálculo direto da força que a esfera exerce sobre o anel está um pouco mais envolvido que o
cálculo da força que o anel exerce na esfera. Essas forças são iguais em magnitude, mas opostas em direção, então será suficiente fazer o último cálculo. Por simetria, a força na esfera estará ao longo do eixo do anel na Figura 12.35 do livro, em direção ao anel.
Divida o anel em elementos infinitesimais com massa .
Passo 2
Cada elemento de massa do anel exerce uma força de magnitude
na esfera, e o componente dessa força é
Portanto, a força na esfera é
na direção -x. A esfera atrai o anel com uma força da mesma magnitude.
Resposta
Como o denominador se aproxima e , como esperado.