Um bloco de oscila preso a uma mola com constante elástica de . Em , o bloco encontra-se à direita da posição de equilíbrio, movendo-se para a esquerda com uma velocidade de . Determine o período de oscilação e desenhe um gráfico posição versus tempo.

Como a gente precisa da amplitude para encontrarmos o período e escrevermos o gráfico, vamos isolar :

Agora a gente substitui cada valor que o enunciado deu:

Com a amplitude, podemos encontrar a velocidade máxima que o bloco pode atingir. A velocidade vai ser máxima exatamente quando o bloco passar pela posição de equilíbrio, porque ali toda a energia potencial da mola foi transformada em energia cinética, e a mola não está mais tensionada.

Nesse caso a equação de energia fica:

E como agora a gente tem a amplitude, basta isolarmos a velocidade máxima:

Substituindo cada valor:

Mas para que encontramos a velocidade máxima?

No movimento harmônico simples, a velocidade máxima de um movimento é dada por:

E com esse a gente pode achar o período das oscilações:

Isolamos :

E substituímos os valores que temos:

Esse vai ser o período das oscilações.

E para o nosso gráfico, basta usarmos a equação de movimento harmônico simples, mas antes precisamos encontrar o valor da fase para escrever ela para o bloco:

Como já temos e , a gente já pode substituir:

Agora para a fase, a gente substitui quando que foi o que o enunciado deu para a gente:

Usando a função arco:

Essa vai ser a fase (em radianos), substituindo na equação de movimento harmonico para o bloco:

Agora a gente tem uma equação pronta para fazermos o gráfico, ele vai ficar assim:

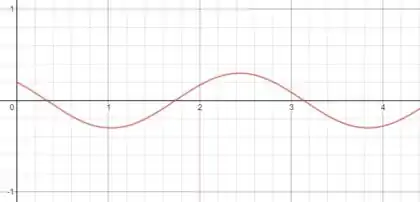
Com o eixo vertical sendo a posição em metros e o horizontal o tempo em segundos.