Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 84
A corda de um pêndulo cônico tem de comprimento e (na sua ponta) uma massa de . (a) Encontre o ângulo entre a corda e a horizontal quando a tensão na corda é seis vezes o peso da massa. (b) Sob essas condições, qual é o período do pêndulo?
Passo 1
No caso do pêndulo cônico nós temos uma massa presa a uma corda em um poste vertical, e seguindo uma trajetória circular na horizontal:
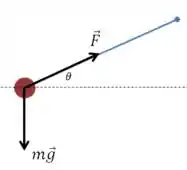
Então queremos que as forças estejam em equilíbrio na direção vertical:
E na direção horizontal precisamos de uma resultante centrípeta:
Passo 2
(a) Além disso, sabemos pelo enunciado que , substituindo no sistema:
E isolando na primeira equação:
Passo 3
(b) Agora queremos calcular o período do pêndulo nesse caso. Esse período está “escondido” naquele da segunda equação do nosso sistema:
E agora é só reescrever do lado direito da equação:
E agora é só calcular o raio do movimento circular usando o comprimento do pêndulo (dê uma olhada na figura):
Substituindo os valores numéricos, ficamos com o seguinte resultado:
Resposta
(a) .
(b) .