Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 96
Como estagiário de engenharia civil, durante um de seus verões na faculdade, solicitam que você desenhe uma seção curva de uma estrada que atende às seguintes condições: quando há gelo na estrada, e o coeficiente de atrito estático entre a estrada e borracha é , um carro em repouso não deve escorregar para dentro da vala e um carro viajando a menos de não deve derrapar para fora da curva. Negligencie os efeitos do arrasto do ar e do atrito de rolamento. Qual é o mínimo raio de curvatura da curva e por qual ângulo a estrada deve ser inclinada?
Passo 1
No caso em que o carro está em repouso, o diagrama de forças fica da seguinte forma:
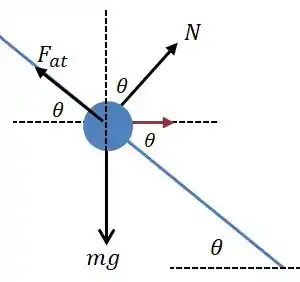
As forças tem que estar em equilíbrio nas duas direções, então:
Como queremos o caso limite, vamos supor que a força já é o máximo atrito que pode haver com a superfície:
Substituindo isso na primeira equação:
Passo 2
Falta calcular o raio de curvatura mínimo da curva. Nesse caso vamos usar o fato de que, quando um carro viaja com , ele está no limite em que não derrapa para fora da curva.
E o nosso diagrama fica um pouco diferente, dessa vez o atrito está agindo justamente para impedir a derrapagem:
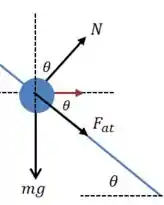
E na direção nós teremos uma resultante centrípeta, ao invés de uma resultante nula.
Vamos substituir nas duas equações e simplificar um pouco:
Temos que resolver esse sistema para encontrar .
Passo 3
Dividindo a segunda equação pela primeira:
Substituindo os valores numéricos:
Resposta
O raio de curvatura deve ser de no mínimo e o ângulo de inclinação deve medir .