Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 7.Problemas - Ex. 50
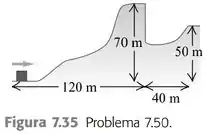
Um bloco de 2,8 kg desliza sobre a colina coberta de gelo e livre de atrito mostrada na Figura 7.35. O topo da colina é horizontal e ergue-se a 70 m da sua base. Qual é a velocidade escalar mínima que o bloco deve ter na base da colina para não cair no vale do outro lado da colina?
Passo 1
Olá, meu querido. Yuri aqui e estarei te ajudando a resolver essa atividade.
Primeiramente precisamos calcular a velocidade mínima que o bloco deve ter para chegar ao outro lado da colina.
Desta forma teremos a velocidade final para posteriormente utilizamos a conservação de energia e determinar a velocidade mínima que o bloco deve ter na base da colina.
Passo 2
Imaginando que o bloco chegue ao outro lado da colina, após o seu salto bem sucedido, isso implica que ele cairá por que é a diferença entre os dois morros(. Desta forma iremos calcular o seu tempo de queda:
diferença de altura
tempo
gravidade
Assim temos que
Passo 3
Agora conhecemos a velocidade mínima que o bloco deve ter no final da colina, podemos usar a conservação de energia para descobrirmos qual deve ser a velocidade na base:
A ao tomar o ponto 1 na base da colina e o ponto 2 no topo da colina, temos:
onde é a altura da colina.
Assim a velocidade inicial será