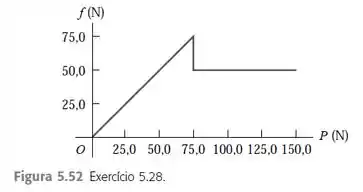
Em um laboratório que conduz experiências sobre atrito, um bloco de repousa sobre uma mesa de superfície horizontal rugosa, que é puxada por um fio horizontal. A força de puxar cresce lentamente até o bloco começar a se mover e continua a aumentar depois disso. A Figura mostra um gráfico da força de atrito que atua sobre esse bloco em função da força de puxar. a) Identifique as regiões do gráfico em que ocorrem o atrito estático e o atrito cinético. b) Ache os coeficientes de atrito estático e cinético entre o bloco e a mesa. c) Por que o gráfico se inclina de baixo para cima na primeira parte, mas depois se nivela? d) Como seria o gráfico, se um tijolo de fosse colocado sobre o bloco e quais seriam os coeficientes de atrito nesse caso?
Passo 1
Fala galera! Beleza?! Bora resolver essa questão!
O enunciado nos deu um gráfico da força de atrito em função da força de puxar de um bloco de que estava repousando sobre uma superfície horizontal rugosa. Então, supondo que essa força cresça lentamente até o bloco começar a se mover e depois continue aumentando, nós precisamos determinar (a) as regiões de atrito cinético e estático do gráfico, (b) os coeficientes de atrito em cada caso, (c) o motivo da inclinação do gráfico ser desse jeito e (d) a forma que ele teria se um tijolo fosse colocado sobre esse bloco.
O gráfico dado é esse aqui:
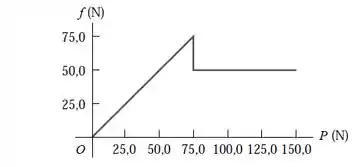
Mas para analisa-lo temos que levar em consideração que a força de atrito também pode atuar quando não existe movimento relativo e para que o objeto comece a se mover a força de tração empregada tem que se tornar maior que o máximo valor da força de atrito estático que a superfície pode exercer. Além disso, a força de atrito estático pode ter qualquer valor entre zero (quando não existe nenhuma outra paralela à superfície) até um valor máximo dado por , ou seja:
E o tipo de atrito que atua quando um corpo está deslizando sobre uma superfície denomina-se atrito cinétio, que é dado pela fórmula:
Onde é o coeficiente de atrito cinético e é a força normal de superfície, nos dois casos.
É com base nessas considerações que avaliar o comportamento do nosso gráfico. Vamos lá!
Passo 2
a) Para determinar as regiões de atrito cinético e estático do gráfico , temos que entender que o bloco inicialmente está em repouso e depois começa a se mover com uma força de tração crescente . Enquanto o bloco está em repouso, não temos nenhum atrito (). Depois que essa força passa a crescer lentamente, um atrito estático é produzido . Isso pode ser visto na primeira parte do gráfico:
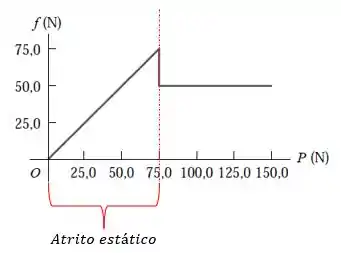
Depois, essa força de atrito atinge um valor máximo e a caixa fica prestes a se mover. Em seguida, o bloco começa a deslizar com uma velocidade escalar constante e passa a ter um atrito cinético :
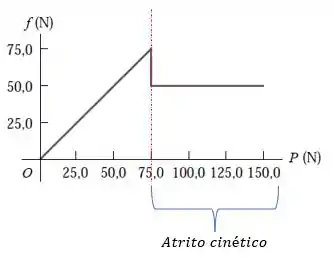
Passo 3
b) Agora vamos achar os coeficientes de atrito estático e cinético entre o bloco e a mesa. Pra isso,
O valor máximo da força de atrito estático é . Do gráfico, temos que isso ocorre em , então usando a fórmula do atrito estático vista no passo , temos:
E substituindo os dados, obtemos:
Passo 4
Da mesma forma, para o atrito cinético, temos:
E pelo gráfico, temos que:
Que é o valor constante que o atrito assume quando o bloco começa a deslizar. Assim, temos o coeficiente de atrito cinético na forma:
E substituindo os valores, obtemos:
Passo 5
c) Como vimos, o gráfico tem uma inclinação na primeira parte, de até , que corresponde a força de atrito estático. Só que em um dado ponto, a força de tração supera a força de atrito e o bloco deixa de estar em equilíbrio para entrar em movimento.
Então, a força supera a máxima força de atrito . Só que quando o deslizamento começa, a força de atrito normalmente diminui, porque manter o bloco deslizando é mais fácil do que produzir o início do movimento e o bloco passa a ter um valor de tração constante. Por isso o gráfico se nivela depois.
Passo 6
d) Se um tijolo de fosse colocado sobre esse bloco, nós teríamos um aumento da força normal de superfície , que seria o dobro do que tínhamos anteriormente.
Sendo assim, tanto o atrito cinético quando o estático dobrariam de valor e os valores de no eixo vertical dobrariam, mas a forma do gráfico permaneceria inalterada, porque os coeficientes de atrito são independentes da força normal.
Valeu, galera! Até a próxima! 😉
Resposta
- O atrito estático ocorre quando até .
- e
O atrito cinético ocorre quando .
c) e d)