Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 6.1 - Ex. 32
Um bloco de 6,0 kg escorrega 15 m abaixo sobre um plano inclinado sem atrito que forma um ângulo de 60º com a horizontal. (a) Desenhe o diagrama de corpo livre para o bloco e encontre o trabalho realizado por cada força, enquanto o bloco escorrega 1 m (medidos ao longo do plano inclinado). (b) Qual é o trabalho total realizado sobre o bloco? (c) Qual é a rapidez do bloco após ter escorregado 15 m, se ele parte do repouso? (d) Qual é sua rapidez, após 15 m, se ele parte com uma rapidez inicial de 2,0 m/s?
Passo 1
Letra (a)
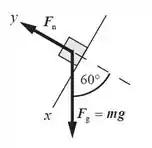
Vamos começar pela força gravitacional. O trabalho de uma força constante é dada por:
Onde é o ângulo entre a força e a direção do deslocamento. Só que força gravitacional é dada por:
Então a equação fica:
Vamos substituir os valores:
Para a força normal, como ela é sempre perpendicular ao deslocamento, o trabalho dela é zero.
Passo 2
Letra (b)
O trabalho total é a soma dos trabalhos:
Passo 3
Letra (c)
Vamos usar o teorema do trabalho-energia:
Mas a energia cinética inicial é nula:
Temos também:
Corta a massa e isola o :
Substitua os valores:
Passo 4
Letra (d)
Se a velocidade inicial não é nula, teremos o seguinte:
Temos também:
Corta a massa e isola o :
Substitua os valores:
Resposta
Letra (a): Força gravitacional = 76 J e força normal = 0 J
Letra (b): 76 J
Letra (c): 5,0 m/s
Letra (d): 5,4 m/s