Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.Problemas Adicionais - Ex. 98
Uma curva circular em uma rodovia é projetada para uma velocidade máxima de . Suponha que os carros não possuem sustentação negativa. (a) Se o raio da curva é , qual é o ângulo de compensação correto? (b) Se a curva não fosse compensada, qual deveria ser o menor coeficiente de atrito entre os pneus e o piso para que os carros não derrapassem ao entrarem na curva a ?
Passo 1
Oá, querido! Tudo bem? Então, temos uma curva por onde os carros precisam passar.
E aí quando a gente fala de curva, a gente fala de movimento com trajetória circular. E sem tem trajetória circular, é necessário que haja um aceleração centrípeta atuando no carro e apontando para o centro da trajetória, para manter o carro no movimento circular.
Ela tem essa expressão:
Onde é o raio da curva.
Só que essa aceleração é produzida pela componente de uma força que atua sobre o carro e aponta para o centro da trajetória. Se a gente considerar que a trajetória é horizontal, a gente precisa de uma componente de uma força que seja horizontal.
E aí uma força que pode fazer esse papel é a componente da força normal . Como assim?
Bem, já percebeu que algumas pistas de corrida são um pouco inclinadas nas curvas? Esse ângulo de inclinação é o ângulo de compensação. Ele faz com que a força normal sobre o carro fique inclinada:
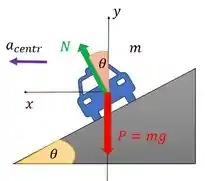
Percebe que se não houvesse essa inclinação, não teria componentes de força na horizontal? Mas com a inclinação, a força que faz papel de força centrípeta é a componente de .
E aí o que ele quer da gente é o valor desse ângulo sabendo que a velocidade na curva é de . Bora lá!
Passo 2
A gente fez um diagrama de corpo livre do carro. E isso não foi só para visualizar o ângulo . Se tem diagrama de corpo livre, a gente aplica a segunda lei de Newton no carro! Para o eixo vamos ter:
Nessa direção não há movimento então . Para cima a gente tem a componente vertical de que vale , porque o ângulo está colado no eixo . E para baixo temos a força peso. Então o somatório fica:
Subtituindo as expressões de cada uma:
Para o eixo :
Nesse caso a gente só tem a componente de que vale e é a aceleração centrípeta que vale . Substituindo essas coisas:
Passo 3
Isolando o na :
Substituindo este valor na :
Assim, isolando
Por fim, para determinar o ângulo de compensação, devemos isolar o ângulo na :
Passo 4
Para substituir os valores dado no enunciado, devemos primeiro converter as unidades.
Perceba que o raio foi dado em metros e a velocidade em quilômetros por hora. Então, vamos passar converter a unidade da velocidade de para , para isso, dividiremos o valor dado por . Assim:
Portanto,
Passo 5
b) Bem, se não há , e a pista é plana, precisamos de outra força que faça o papel de força centrípeta. A força vai ser a força de atrito entre os pneus do carro e pista.
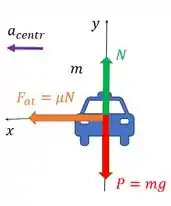
Aí ele quer saber o valor de coeficiente de atrito nesse caso . Vamos usar a segunda lei de Newton de novo. Para o eixo :
Passo 6
E no eixo :
E aqui só temos a força de atrito que vale e a aceleração centrípeta :
Portanto, substituindo na a :
Isolando :
Resposta
- ;
- .