Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.Problemas Adicionais - Ex. 65
Um bloco de massa é colocado em cima de um outro bloco de massa . Para fazer o bloco de cima deslizar sobre o bloco de baixo enquanto o segundo é mantido fixo, é preciso aplicar ao bloco de cima uma força horizontal de no mínimo . O conjunto de blocos é colocado sobre uma mesa horizontal sem atrito (Fig. 6-47). Determine o módulo (a) da maior força horizontal que pode ser aplicada ao bloco de baixo sem que os blocos deixem de se mover juntos e (b) a aceleração resultante dos blocos
Passo 1
Então galera , o sistema é formado por duas caixas, uma em cima da outra. O nosso objetivo é calcular a força máxima que pode ser aplicada sem que os blocos deixem de se mover juntos . Para isso , temos que construir os diagramas de corpo livre dos dois blocos :
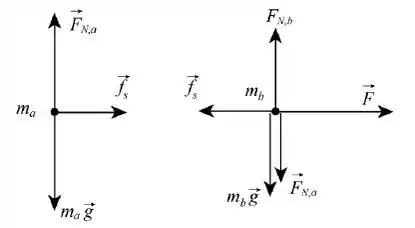
Em primeiro lugar, calculamos o coeficiente de atrito estático da superfície entre os dois blocos. Como uma força de no mínimo deve ser aplicada ao bloco de cima para que deslize, e , portanto,
Até aqui de boa , pessoal?
Usando o mesmo raciocínio, para que os dois blocos se movam juntos, a força aplicada ao bloco de baixo não deve ser maior que:
A última equação nos dá :
Passo 2
Nós sabemos que a aceleração máxima com a qual os blocos se movem juntos é obtida através da relação :
Resposta
Tranquilo galera?? Bora resolver mais questões então