Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.3 - Ex. 28
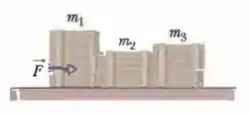
A Fig. 6-32 mostra três caixotes sendo empurrados sobre um piso de concreto por uma força horizontal de módulo . As massas dos caixotes são , e . O coeficiente de atrito cinético entre o piso e cada um dos caixotes é de . (a) Qual é o módulo da força exercida sobre o bloco pelo bloco ? (b) Se os caixotes deslizassem sobre um piso polido, com um coeficiente de atrito cinético menor que , o módulo seria maior, menor ou igual ao valor quando o coeficiente de atrito era ?
Passo 1
Belezera pessoal, vamos começar essa questão fazendo um diagrama do corpo livre para o sistema formado pelo caixote e , e para o sistema formado pelos três caixotes, respectivamente:
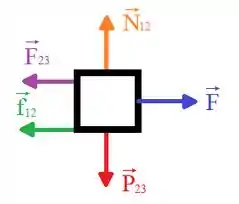
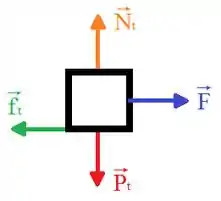
Lembrando que podemos calcular a força de atrito cinético através da seguinte relação:
Um ponto importante que podemos observar para facilitar nosso desenvolvimento é que no eixo , perpendicular a força , de todos os caixotes somente duas forças atuam: A força peso e a força normal. E como o eixo está em equilíbrio, então:
Portanto, podemos juntar as duas equações, de maneira que:
Passo 2
Aplicando a segunda lei de Newton no sistema formado pelo caixote e no eixo :
Isolando o :
Substituindo a equação da força de atrito , obtemos que:
Passo 3
Iradoso, agora aplicando a segunda lei de Newton para o sistema formado pelos três caixotes:
Isolando :
Tal que:
Passo 4
Como as acelerações tem de serem iguais, obtemos a seguinte relação:
Isolando :
Substituindo os valores conhecidos:
Passo 5
Pela terceira lei de Newton, sabemos que o módulo de é igual ao módulo de que foi calculado anteriormente, então:
Passo 6
Pela equação da força :
Percebemos que o módulo da força só depende das massas dos caixotes e da força , então se mudar o não mudará o módulo de .
Resposta
- ;
- .