Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 1- Ed: 10º - Capítulo 7.Problemas - Ex. 64

Uma mola com massa desprezível e constante k é comprimida de uma distância x por uma caixa de massa m. A caixa é libertada e sobre uma rampa inclinada de um ângulo α acima da horizontal. O coeficiente de atrito cinético entre a caixa e a rampa é μ c , onde μ c   < 1 . A caixa ainda sobe a rampa depois de deslocar uma distância s   >   | x | ao longo da rampa. Calcule o ângulo α para o qual a velocidade da caixa atinge seu valor mínimo depois de ela se deslocar uma distância s. Explique por que a velocidade mínima não ocorre para α =   90 , embora para este α exista um aumento máximo da energia potencial gravitacional.

Passo 1

Beleza pessoal?! Espero que esteja tudo bem com meu os herdeiros de Newton. Vamos dar início a mais uma resolução com o padrão de qualidade do Responde aí, então pegue seu lápis, caderno e café e vamos nessa!!!

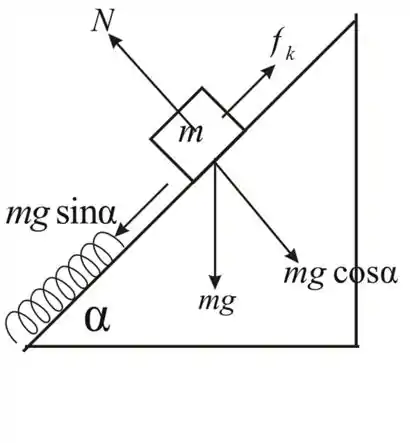
O trabalho realizado pela gravidade e fricção:

Da figura acima, a equação da força é:

F   = f k   - m g   s i n   α   ( 1 )

a força de atrito é:

f k = - μ c N

N   =   m g s i n   α

F   =   - μ c m g c o s   α   -   m g s i n   α

Passo 2

O trabalho feito pelo bloco em uma distância x é:

W   =   - m g ( s i n   α   +   μ c   c o s   α ) s

A energia potencial é de:

P   =   0.5 k x ²

a energia cinética depois de subir uma distância s na rampa acima será de:

K 1   =   0.5 k x ²   -   m g ( s i n α + μ c c o s   α ) s  

A velocidade será mínima quando a energia cinética for mínima:

d K 1 d α = 0

- m g s ( c o s α -   μ s   s i n   α ) = 0

α   =   t a n ⁻ ¹ ( 1 μ k )

Resposta

α   =   t a n ⁻ ¹ ( 1 μ k )

Exercícios de Livros Relacionados

Um carrinho de plástico de 0,2 kg e outro, feito de chumbo de 20 kg, deslocam-se sem atrito sobre uma superfície horizontal. Forças iguais são empregadas para empurrar os dois por uma distância de 1m,
Você precisa erguer um bloco pesado puxando-o por meio de uma corda desprovida de massa. Você pode (a) puxar o bloco diretamente pra cima até a altura h ou (b) puxá-lo ao longo de um plano inclinado e
Você solta uma bola de uma sacada alta e ela imediatamente cai. A energia cinética da bola aumenta em quantidades iguais durante intervalos de tempo iguais ou aumenta em quantidades iguais durante dis
Bob consegue arremessar uma pedra de 500g a 30m / s . Ao fazer isso, ele movimenta sua mão para a frente ao longo de 1,0m . a. Quanto trabalho a mão de Bob realiza sobre a pedra? b. Que valor de força
Um elevador de 1.000k g acelera a 1,0m / s 2 por 10m de subida, tendo partido do repouso. a. Quanto trabalho realiza a gravidade sobre o elevador? b. Quanto trabalho realiza a tensão no cabo sobre o e