Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 1- Ed: 10º - Capítulo 7.Problemas - Ex. 69

Uma força conservativa F atuando ao longo do eixo Ox e uma força dada pela lei de Hooke

atuam sobre um íon.

a) Mostre que uma possível função energia potencial para a combinação dessas forças é dada por

Essa é a única função possível? Explique.

b) Ache a posição do equilíbrio estável.

c) Faça um gráfico de U(x) (em unidades de) versus x (em unidades de) para valores de x entre

e .

d) Existe alguma posição de equilíbrio instável?

e) Quando a energia total for, qual será o valor máximo e o valor mínimo de x para o movimento do íon?

f) Sendo m a massa do íon, determine sua velocidade máxima quando a energia total for

. Para qual valor de x sua velocidade é máxima?

Passo 1

Digamos que temos um átomo ou íon negativo. O íon sofre a ação de uma força de gancho conservativa. Na primeira parte, temos que mostrar como é a força se tivermos potencial. Depois disso, procuramos pontos de equilíbrio estáveis. No final, procuramos as distâncias mínima e máxima dos íons quando eles se movem.

  1. A partir do potencial dado U   =   k x ² 2 - F x - F ² 2 k temos que encontrar a expressão para a força, vamos procurá-la usando um gradiente. A energia potencial e a força estão relacionadas através de um gradiente da seguinte forma

F _ = ∇ U

= ∂ u ∂ x î

= ∂ ( k x ² 2 - F x - F ² 2 k ) ∂ x î

= ( - k x + F ) î

Este não é um termo exclusivo para potencial. Na expressão do potencial podemos sempre adicionar uma constante que depende da situação física sem alterar a força.

Passo 2

b) Encontraremos pontos de equilíbrio estáveis ​​quando derivarmos o potencial:

d U d x = 0

d U d x = - k x 0 = F

x 0 = F k

O potencial no ponto de equilíbrio é:

U ( x 0 ) = k x 0 ² 2 - F x 0 - F 2 k

c) Quando desenhamos esse potencial em unidades: F ² k ​ o potencial se torna:

U ( x ) = k x ² 2 - F x - F ² 2 k

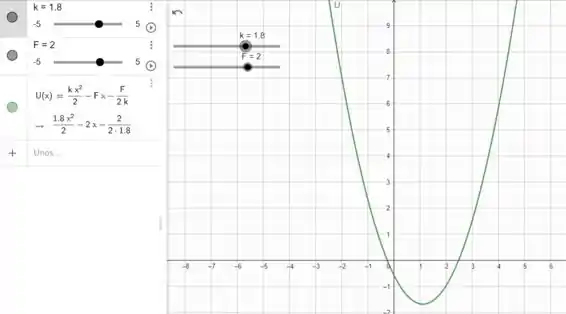
Passo 3

d) Pelo gráfico podemos ver claramente que não há pontos instáveis ​​no potencial.

e)Se a energia total é E = F ² k vamos calcular as distâncias mínima e máxima dos íons a partir da posição de equilíbrio. Obteremos isso se olharmos para o gráfico abaixo, encontrando os pontos de interseção da energia potencial e total.

F ² k ( k ² ∙ x ² 2 F ² - k F x - 1 2 ) = F ² k

k ² x ² 2 F ² - k F x - 3 2 = 0

x 1 = - F k

x 2 = 3 F k

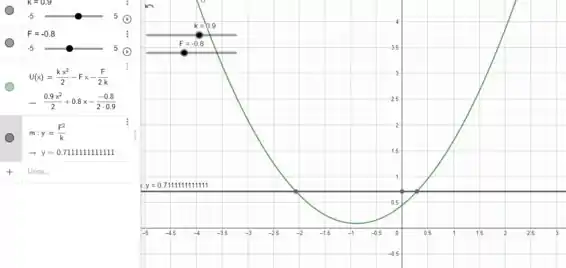
Se o íon tem massa m, encontre a velocidade máxima se a energia total é: E = F ² k ​, a energia cinética máxima é quando o íon passa pelo potencial mínimo, ou seja, no ponto x 0 = F k ​:

K = E - U

K = F ² k - ( - F ² k )

K = 2 F ² k

m v ² 2 = 2 F ² k

v = 2 F m k

Resposta

  1. F = ( - k x + F ) î
  2. U ( x 0 ) = - F ² k
  3. U ( x ) = k x ² 2 - F x - F ² 2 k
  4. x 1 = - F k

    5. x 2 = 3 F k

  5. v = 2 F m k

Exercícios de Livros Relacionados

Um cabo uniforme, de massa M e coprimento L, está inicialmente equilibrado sobre uma pequena polia de massa desprezível, com a metade do cabo pendente de cada lado da polia. Devido a um pequeno desequ
Um garoto que atirar um pedregulho de massa igual a 50g num passarinho pousado num galho 5m a sua frente e 2m acima do seu braço. Para isso utiliza um estilingue em que cada elástico se estica de 1cm
Uma partícula de massa m=2Kg desloca-se ao longo de uma reta. Entre x=0 e x=7 m, ela está sujeita à força F(x) representada no gráfico. Calcule a velocidade da partícula depois de percorrer 2,3,4,6 e
Uma bolinha amarrad a um fio e comprimento l = 1 m gira num plano vertical. a) Qual deve ser a velocidade da bolinha no ponto mais baixo B (Fig.) para que ela descreva o círculo completo? b) A velocid
Calcule o produto escalar vec A . vec B se:vec A = 4 vec i + 2 vec j e vec B = - 3 vec i - 2 vec j vec A = - 4 vec i + 2 vec j e vec B = - vec i - 2 vec j