Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 7.Problemas - Ex. 8

Uma partícula está confinada a mover-se no semi-espaço z ≥   0   , sob a ação de forças conservativas, de energia potencial U x , y , z = F 0 z + 1 2 k x 2 + y 2 , onde F 0   e   k são positivas. a) Calcule as componentes da força que atua sobre a partícula. b) Que tipo de força atua ao longo do eixo Oz? c) Que tipo de forças atuam no plano xy? Qual é a forma das superfícies equipotenciais?

Passo 1

    2. F x =   - d U d x

    = -   k x

    F y = - d U d y  

    =   - k y

    F z = - d U d z

    =   - F 0

    Passo 2

  2. No eixo z atua uma força constante com sentido para baixo

    3. Passo 3

  3. Forças correspondentes à força elástica atuam no plano xy.

    4. Passo 4

  4. Para descobrir as superfícies equipotenciais vamos igualar nossa funçãozinha de ponteical à uma constante, chega mais

F 0 z + 1 2 k x 2 + y 2 = C

z =   - k 2 F 0 x 2 + y 2 + C

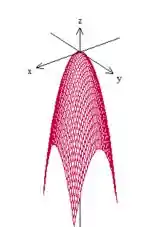
Esse resultado representa um conjunto de paraboloides de revolução com concavidade para baixo! Vamos ver o gráfico de um deles

Resposta

a )   F ⃑ = ( - k x ,   - k y ,   - F 0 )

b ) F o r ç a   c o n s t a n t e

c )   F o r ç a   e l á s t i c a

d )   P a r a b o l ó i d e s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quanta energia total é armazenada no lago do Problema 7.79? Como naquele problema, considere a energia potencial gravitacional como igual a zero na base da represa. Expresse suaresposta em joules e em
Uma força conservativa F atuando ao longo do eixo Ox e uma força dada pela lei de Hooke F = - k x atuam sobre um íon.a) Mostre que uma possível função energia potencial para a combinação dessas forças
Um bloco de gelo de 0,150 kg é colocado contra uma mola horizontal comprimida no alto de uma mesa de altura 1,20 m acima do solo. A mola está inicialmente comprimida 0,045 m e a constante da mola é ig
Um dispositivo experimental de massa m está apoiado sobre uma mola vertical com massa desprezível e empurrado para baixo até que a mola seja comprimida de uma distância x. O dispositivo é então libert
Uma usina hidrelétrica represa as águas de um lago com área de superfície de 3,0 × 10 6m 2 , que possui laterais verticais abaixo do nível da água. Esse nível fica 150 m acima da base da represa. Quan