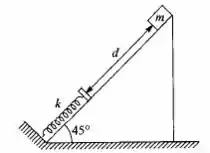
Um bloco de massa é solto em repouso do alto de um plano inclinado de em relação ao plano horizontal, com coeficiente de atrito cinético Depois de percorrer uma distância d=2m ao longo do plano, o bloco colide com uma mola de constante k=800 N/m, de massa desprezível, que se encontrava relaxada. a) Qual é a compressão sofrida pela mola? b) Qual é a energia dissipada pelo atrito até a compressão máxima da mola? Que fração representa da variação total de energia potencial durante o trajeto? c) Se o coeficiente de atrito estático com o plano é , que acontece com o bloco logo após colidir com a mola?
Passo 1
- Pra saber a compressão da mola é preciso saber nossa energia mecânica no ínicio da compressão, beleza? Então bora dividir o problema em 2 etapas.
- Antes da mola
- Interação com a mola
Vamos lá, a energia mecânica inicial é perdida em parte devido ao atrito, colocando isso em uma fórmula fica assim
Sabemos que o trabalho do atrito é dissipativo e portanto negativo na nossa fórmula, de modo que a energia mecânica final é menor. A energia mecânica inicial era só gravitacional, então fica assim
Como vamos substituir na fórmula de cima e colocar o que tem em comum em evidência,
Apenas substituindo os valores que temos, concluímos que
Aqui a variação da energia mecânica da nossa massa ocorrerá devido ao atrito e à transferência de energia para a mola se comprimir, show? Então temos
Se liga que aqui nossa energia mecânica final é só energia potencial gravitacional, já que queremos a compressão máxima da mola, ou seja, quando a velocidade do bloquinho chegar a 0 e .
Pra gente não se confundir vamos pensar agora que na posição de equilíbrio da mola o potencial gravitacional é 0, então se o bloquinho desceu uma altura até a compressão total da mola seu deslocamento foi de
Portando a variação de energia mecânica é
Usando a mesma relação entre a altura e o deslocamento no plano temos
Além disso tudo aí, o resto da equação fica assim
Escrevendo no formato de equação de segundo grau,
Passo 2
Passo 3
Passo 4
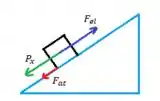
Por esse resultado vemos que a força elástica é bem maior que o atrito estático e a componente do peso, jogando o bloco de volta pra cima do plano.