Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 10.9 - Ex. 54a
Na figura abaixo, um cilindro com uma massa de pode girar em torno do eixo central, que passa pelo ponto O. As forças mostradas têm os seguintes módulos: , , e . As distâncias radiais são e . Determine (a) o módulo e (b) a orientação da aceleração angular do cilindro. (Durante a rotação, as forças mantêm os mesmos ângulos em relação ao cilindro).
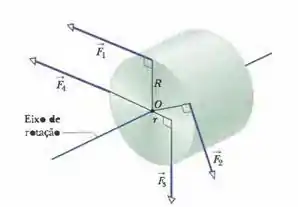
Letra (a)
Passo 1
Usando as convenções de sinais adotadas pelo livro (Halliday), o módulo do torque resultante a que o cilindro está submetido é:
E a aceleração do cilindro tabelada é:
Onde
Passo 2
Substituindo os valores das forças para calcular o torque, temos:
A aceleração torna-se:
Resposta
Exercícios de Livros Relacionados
Três forças são aplicadas a uma roda com raio igual a 0,350 m, conforme mostra a Figura 10.40. Uma força é perpendicular à borda, outra é tangente a ela e a outra forma um ângulode 40 ° com o raio. Qu
Uma placa metálica quadrada de lado igual a 0,180m possui um eixo pivotado perpendicularmente ao plano da página passando em seu centro O (Figura 10.39). Calcule o torque resultante em torno desse eix
Uma barra horizontal fina de comprimento l e massa M é articulada em torno de um eixo vertical passando em sua extremidade. Uma força com módulo constante F é aplicada à outraextremidade, fazendo a ba
O volante de certa máquina possui momento de inércia igual a 2,50k g ⋅ m 2 em torno do seu eixo de rotação. Qual é o torque constante necessário para que, partindo do repouso, sua velocidade angular a
Uma casca esférica uniforme de 8,40 kg e 50,0 cm de diâmetro possui quatro pequenas massas de 2,0 kg presas à superfície externa e igualmente espaçadas entre si. Esse sistema está girando em torno de