Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 15.2 - Ex. 33
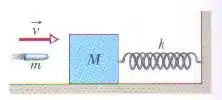
Um bloco de massa , em repouso em uma mesa horizontal sem atrito, está ligado a um suporte rígido através de uma mola de constante elástica . Uma bala de massa e velocidade de módulo atinge o bloco e fica alojada nele (Figura). Supondo que a compressão da mola é desprezível até a bala se alojar no bloco, determine (a) a velocidade do bloco imediatamente após a colisão e (b) a amplitude do movimento harmônico simples resultante.
Passo 1
Fala galerinha bonita, tudo beleza?
(a) Essa parte nem envolve oscilações, é apenas uma questão de conservação de momento linear.
Então vamos lá, o momento linear inicial é dado como:
Mas a velocidade do bloco maior é zero, com e , ou seja:
E o momento linear final, é:
Estamos considerando os dois corpos como se fossem um só, já que a bala fica “alojada” no bloco maior.
Pela conservação de momento linear:
Logo:
Passo 2
(b) Agora queremos saber a amplitude do movimento.
Uma das formas de calcular isso, é descobrindo a energia total do movimento, nesse caso, poderíamos igualar:
Então beleza, vamos tentar achar isso. Acabamos de calcular que, no momento em que a bala entra no bloco, os dois partem com velocidade:
E o enunciado diz que, logo antes da colisão, o bloco estava em repouso, isso quer dizer que a mola não estava comprimida nem esticada, e então a energia potencial é nula:
Tal que:
Passo 3
Beleza, agora podemos substituir esses valores na fórmula de cima pra achar a amplitude:
Portanto:
Resposta
(a)
(b)