Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 7.1 - Ex. 94
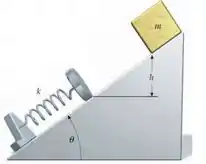
Um bloco de massa parte do repouso a uma altura e escorrega para baixo sobre um plano sem atrito inclinado de um ângulo com a horizontal, como mostra a figura. O bloco atinge uma mola de constante de força . Determine de quanto a mola é comprimida até o bloco parar momentaneamente.
Passo 1
Vamos aplicar a conservação de energia entre dois instantes: o primeiro quando o bloco está parado no topo da altura , e o segundo quando está parado no ponto de máxima compressão da mola.
Perceba que nesses dois pontos a energia cinética é zero. E vamos definir o zero da nossa energia potencial gravitacional como sendo a altura do ponto de máxima compressão da mola.
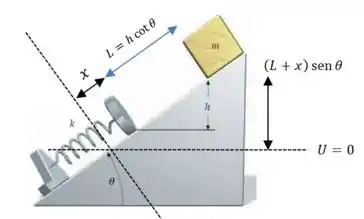
Passo 2
Então inicialmente, quando o bloco tem apenas energia potencial gravitacional, a energia mecânica total do sistema é:
Mais tarde, quando a mola tiver sido comprimida por uma distância , a energia mecânica do sistema será:
Já que não haverá mais energia potencial gravitacional, e nem cinética.
Passo 3
Pela conservação de energia:
E nosso objetivo é encontrar , então vamos reescrever:
E resolvendo essa equação do segundo grau:
E então:
E podemos excluir a raiz negativa e substituir a expressão que criamos para :
Resposta
A distância pela qual a mola é comprimida até parar completamente é .