Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 7.1 - Ex. 95

Um bloco de massa m está suspenso por uma mola e é livre para se mover verticalmente (veja a figura). A orientação + y aponta para baixo e a origem está na posição do blcoo quando a mola está frouxa. (a) Mostre que a energia potencial como função da posição pode ser expressa como U = 1 2 k y 2 - m g y . (b) Usando um programa de planilha eletrônica, ou uma calculadora gráfica, faça um gráfico de U como função de y com k = 2   N / m e m g = 1   N . (c) Explique como se pode ver, no gráfico, que existe uma posição de equilíbrio estável para um valor positivo de y . Usando a expressão para U da parte (a), determine (analiticamente) o valor de y quando o bloco está em sua posição de equilíbrio. (d) Da expressão para U , encontre a força resultante que atua sobre m em qualquer posição y . (e) O bloco é largado do repouso com a mola frouxa; se não existe atrito, qual é o maior valor de y que ele atingirá? Indique y m á x em seu gráfico/planilha.

Passo 1

(a) Existem duas fontes de energia potencial nesse sistema: a energia potencial elástica e a potencial gravitacional.

U e l = 1 2 k y 2

U g = - m g y

E o sinal negativo aparece na gravitacional porque ela diminui quando y aumenta, e definimos U = 0 como a altura do ponto em que a mola está frouxa.

Então a energia potencial do sistema é:

U = 1 2 k y 2 - m g y

Passo 2

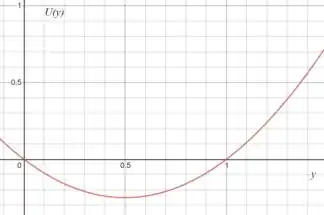
Vamos fazer o gráfico dessa função em uma calculadora gráfica:

U y = 1 2 k y 2 - m g y

U y = 1 2 2   N / m y 2 - 1   N y

U y = y 2 - y

Passo 3

(c) Olhando para o gráfico, podemos ver uma posição de equilíbrio estável em y = 0,5 , que é um ponto de mínimo da função.

Se o objeto estiver naquela posição, a sua tendência será de permanecer ali, pois ao caminhar em qualquer outra direção (aumentando ou diminuindo y , haverá uma força empurrando-o de volta).

Podemos determinar esse ponto analiticamente se buscarmos um extremo da função U ( y ) :

U y = 1 2 k y 2 - m g y

d U d y = k y - m g

E igualando essa derivada a zero:

k y = m g

y = m g k

Colocando os valores que foram usados na construção do gráfico:

y = 1 2 = 0,5

O que concorda exatamente com o que vemos no gráfico.

Passo 4

(d) Para encontrar a força a partir da expressão do potencial, podemos usar a seguinte fórmula:

F = - d U d y

F = - d d y 1 2 k y 2 - m g y  

F = - k y + m g

Passo 5

(e) A melhor forma de encontrar y m á x é analisando nosso gráfico.

Se o objeto é solto a partir do repouso, com a mola frouxa, e a partir da altura que nós decidimos marcar com U = 0 , então a energia mecânica inicial do sistema é nula.

Como a energia se conserva, a energia mecânica do sistema deve permanecer menor do que zero a todo momento.

Isso quer dizer que, no nosso gráfico, os estados permitidos são apenas aqueles que estão abaixo dessa reta azul pontilhada em que U = 0 :

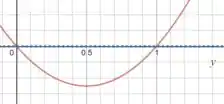
Entre esses estados permitidos, o maior valor de y é y = 1   m , portanto:

y m á x = 1   m

Resolvendo isso de forma analítica, só precisamos considerar:

U = 1 2 k y 2 - m g y = 0

y k y - 2 m g = 0

E as duas soluções são:

y = 0

k y - 2 m g = 0         ⇒         y = 2 m g k

Como estamos em busca do y máximo, ficamos com:

y m á x = 2 m g k

Resposta

(a) Demonstração.

(b) Gráfico.

(c) y 0 = m g / k .

(d) F = - k y + m g .

(e) y m á x = 2 m g / k .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A energia potencial entre dois átomos em uma molécula diatômica é dada por U r =a r 12 -b r 6 , onde r é a distância entre os átomos e a e b são constantes positivas. a) Determine a força F ( r ) que
Dois blocos com massas diferentes estão amarrados a cada extremidade de uma corda leve que passa sobre uma polia leve e sem atrito, que está suspensa a partir do teto. As massas são libertadas do repo
Em um canteiro de obras, um balde de concreto de 65k g está suspenso por um cabo leve (porém forte), que passa sobre um polia leve sem atrito e está conectado a uma caixa de 80,0k g sobre um teto hori
Um carro em um parque de diversões se desloca sem atrito ao longo do trilho indicado na Figura 7.32. Ele parte do repouso no ponto A situado a uma altura h acima da base do círculo. Considere o carro
Uma única força conservativa paralela ao eixo O x atua sobre uma partícula que se desloca ao longo do eixo O x . A força corresponde ao gráfico de energia potencial indicado na F i g u r a7.45 . A par